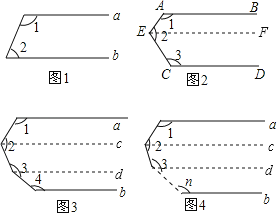
【题目】(1)如图1,a∥b,则∠1+∠2=
(2)如图2,AB∥CD,则∠1+∠2+∠3= ,并说明理由
(3)如图3,a∥b,则∠1+∠2+∠3+∠4=
(4)如图4,a∥b,根据以上结论,试探究∠1+∠2+∠3+∠4+…+∠n= (直接写出你的结论,无需说明理由)
参考答案:
【答案】故答案为:180°;360°;540°;(n﹣1)180°
【解析】
(1)根据两直线平行,同旁内角互补得出答案;(2)过点E作EF∥AB,根据平行线的性质得出答案;(3)过∠2、∠3的顶点作a的平行线,然后根据平行线的性质得出答案;(4)过∠2、∠3…的顶点作a的平行线,然后根据平行线的性质得出答案.
(1)∵a∥b,
∴∠1+∠2=180°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠AEF=180°,∠CEF+∠2=180°,
∴∠1+∠AEF+∠CEF+∠2=180°+180°,
即∠1+∠2+∠3=360°;
(3)如图,过∠2、∠3的顶点作a的平行线,
则∠1+∠2+∠3+∠4=180°×3=540°;
(4)如图,过∠2、∠3…的顶点作a的平行线,
则∠1+∠2+∠3+∠4+…+∠n=(n﹣1)180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.

(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,cos∠ABC=
 ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A,B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.

(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )

A.27°B.59°C.69°D.79°
-
科目: 来源: 题型:
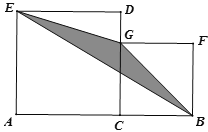
查看答案和解析>>【题目】如图,点C是线段AB上的一点,分别以AC.BC为边在AB的同侧作正方形ACDE和正方形CBFG,连接EG.BG.BE,当BC=1时,△BEG的面积记为S1,当BC=2时,△BEG的面积记为S2,……,以此类推,当BC=n时,△BEG的面积记为Sn,则S2020-S2019的值为____.
相关试题

