【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
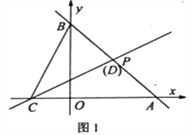
(2)点C为x轴负半轴上一点,过点C的直线l2:![]() 交线段AB于点D。
交线段AB于点D。
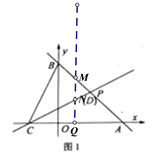
如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若![]() ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;
如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。

参考答案:
【答案】(1) ![]() ;(2)①
;(2)①![]() ,
,![]() ;②
;②![]()
【解析】(1)用待定系数法求解;(2)点Q的位置有两种情况:当点Q在点A左侧,点P的右侧时![]() ;当点Q在点P的右侧时,
;当点Q在点P的右侧时,![]() .都有
.都有![]() ,再根据MN=2MQ,可求t的值;(3)由BC=CD,证△BCO≌△CDE,设C(a,0),D(4+a,-a),并代入解析式,通过解方程组可得.
,再根据MN=2MQ,可求t的值;(3)由BC=CD,证△BCO≌△CDE,设C(a,0),D(4+a,-a),并代入解析式,通过解方程组可得.
解:(1)设直线l1的解析式为y=kx+b,
直线![]() 经过点P(2,2),A(4,0),
经过点P(2,2),A(4,0),
即![]() , 解得
, 解得![]() ,
,
直线l1的解析式为y=-x+4;
(2)①∵直线l2过点P(2,2)且![]() ,
,
即直线l2:![]() ,
,
点Q(t,0),M(t,4-t),N(t,![]() ),
),
1. 当点Q在点A左侧,点P的右侧时,
![]() ,
,![]() ,
,
即![]() ,解得
,解得![]() ;
;
⒉ 当点Q在点A右侧时
![]() ,MQ=t-4,
,MQ=t-4,
即![]() ,解得t=10,
,解得t=10,
②过点D作DE⊥AC于E ,
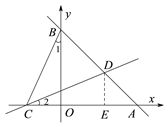
∵BC=CD,BO=OA,
∠DBC=∠1+∠ABO=∠BDC=∠2+∠DAE,
∴∠1=∠2,
∴△BCO≌△CDE,
∴OC=ED,BO=CE,
设C(a,0),D(4+a,-a),
则![]() ,
,
解得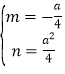 ,
,
即![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 .
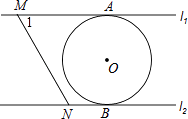
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数分别为_____和_____,p的值为_____.若以C为原点,p的值为_____;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p;
(3)若原点O在图中数轴上点C的右边,且CO=a,求p(用含a的代数式表示).
(4)若原点O在图中数轴上线段BC上,且CO=a,求p(用含a的代数式表示).利用此结果计算当a=0.5时,p的值.
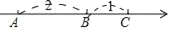
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+
 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 . 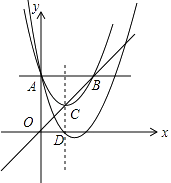
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,正比例函数y=kx与一次函数y=-kx-k(k≠0)的大致图象是( )
A.
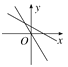 B.
B. 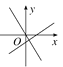 C.
C.  D.
D. 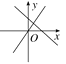
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、C、N三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,则∠BCM:∠BCN=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x=150°时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________.
相关试题

