【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数分别为_____和_____,p的值为_____.若以C为原点,p的值为_____;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p;
(3)若原点O在图中数轴上点C的右边,且CO=a,求p(用含a的代数式表示).
(4)若原点O在图中数轴上线段BC上,且CO=a,求p(用含a的代数式表示).利用此结果计算当a=0.5时,p的值.
![]()
参考答案:
【答案】(1)﹣2、1、﹣1、﹣4;(2)-88;(3)p=﹣3a﹣4;(4)p= 3a﹣4,当a=0.5时,p=﹣2.5.
【解析】
(1)根据以B为原点,则C表示1,A表示﹣2,进而得到p的值;根据以C为原点,则A表示﹣3,B表示﹣1,进而得到p的值;
(2)根据原点O在图中数轴上点C的右边,且CO=28,可得C表示﹣28,B表示﹣29,A表示﹣31,据此可得p的值.
(3)若原点O在图中数轴上点C的右边,且CO=a,可得C的值为﹣a,B的值为﹣a﹣1,A的值为﹣a﹣3,据此可得p的值;
(4)若原点O在图中数轴上线段BC上,且CO=a,可得C的值为a,B的值为﹣(1﹣a)=a﹣1,A的值为a﹣3,据此得出p的值,代入计算可得答案.
(1)若以B为原点,则点A所对应的数为﹣2、点C对应的数为1,此时p=﹣2+0+1=﹣1;
若以C为原点,则点A所对应的数为﹣3、点B对应的数为﹣1,此时p=﹣3﹣1+0=﹣4.
故答案为:﹣2、1、﹣1、﹣4;
(2)根据题意知,C的值为﹣28,B的值为﹣29,A的值为﹣31,则p=﹣28﹣29﹣31=﹣88;
(3)根据题意知,C的值为﹣a,B的值为﹣a﹣1,A的值为﹣a﹣3,则p=﹣a﹣a﹣1﹣a﹣3=﹣3a﹣4;
(4)根据题意知,C的值为a,B的值为﹣(1﹣a)=a﹣1,A的值为a﹣3,p=a+a﹣1+a﹣3=3a﹣4,当a=0.5时,p=3×0.5﹣4=﹣2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求
 的值;
的值;若AD=3,则OE的长为_________(直接写出结果).


-
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
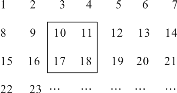
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
-
科目: 来源: 题型:
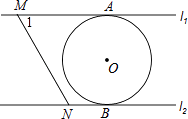
查看答案和解析>>【题目】如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+
 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 . 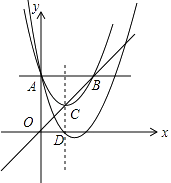
-
科目: 来源: 题型:
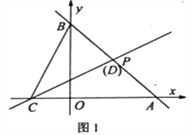
查看答案和解析>>【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:
 交线段AB于点D。
交线段AB于点D。如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若
 ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,正比例函数y=kx与一次函数y=-kx-k(k≠0)的大致图象是( )
A.
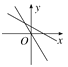 B.
B. 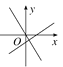 C.
C.  D.
D. 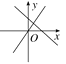
相关试题

