Question

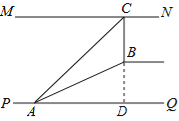
【题目】如图①，某超市从一楼到二楼有一自动扶梯，图②是侧面示意图．已知自动扶梯AB的坡度为1∶2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，则二楼的层高BC约为(精确到0.1米，sin42°≈0.67，tan42°≈0.90)(　　)

A. 10.8米 B. 8.9米 C. 8.0米 D. 5.8米

Answer 1

【答案】D

【解析】试题分析：延长CB交PQ于点D，根据坡度的定义即可求得BD的长，然后在直角△CDA中利用三角函数即可求得CD的长，则BC即可得到．

解：延长CB交PQ于点D．

∵MN∥PQ，BC⊥MN，

∴BC⊥PQ．

∵自动扶梯AB的坡度为1：2.4，

∴==．

设BD=5k（米），AD=12k（米），则AB=13k（米）．

∵AB=13（米），

∴k=1，

∴BD=5（米），AD=12（米）．

在Rt△CDA中，∠CDA=90゜，∠CAD=42°，

∴CD=ADtan∠CAD≈12×0.90≈10.8（米），

∴BC=10.8﹣5≈5.8（米）．

故选：D．