【题目】一组数据x1,x2,…,xn的平均数为5,方差为16,其中n是正整数,则另一组数据3x1+2,3x2+2,…,3xn+2的平均数和标准差分别是( )
A. 15,144 B. 17,144 C. 17,12 D. 7,16
参考答案:
【答案】C
【解析】
根据标准差的概念计算.先表示出数据x1、x2、x3、x4、x5的平均数,方差;然后表示新数据的平均数和方差,通过代数式的变形即可求得新数据的平均数和方差.
∵x1,x2,…,xn的平均数是5,则x1+x2+…+xn=5n,
∴![]() =
=![]() [(3x1+2)+…+(3xn+2)]=
[(3x1+2)+…+(3xn+2)]=![]() [3×(x1+x2+…+xn)+2n]=17,
[3×(x1+x2+…+xn)+2n]=17,
![]() =
=![]() [(3x1+2-17)2+(3x2+2-17)2+…+(3xn+2-17)2]
[(3x1+2-17)2+(3x2+2-17)2+…+(3xn+2-17)2]
=![]() [(3x1-15)2+…+(3xn-15)2]=9×
[(3x1-15)2+…+(3xn-15)2]=9×![]() [(x1-5)2+(x2-5)2+…+(xn-5)2]=144,
[(x1-5)2+(x2-5)2+…+(xn-5)2]=144,
∴标准差为12,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一“过关游戏”,规定:在第n关要掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于
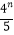 ,则算过关,否则不算过关.
,则算过关,否则不算过关.
(1)过第1关是事件(填“必然”、“不可能”或“不确定”,后同),过第4关是事件;
(2)当n=2时,计算过过第二关的概率(可借助表格或树状图). -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
直线y=
 x+6和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作长方形ABCD,AB:BC=3:4.
x+6和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作长方形ABCD,AB:BC=3:4.(1)当点A与点F重合时(图1),求证:四边形ADBE是平行四边形,并求直线DE的表达式;
(2)当点A不与点F重合时(图2),四边形ADBE仍然是平行四边形?说明理由,此时你还能求出直线DE的表达式吗?若能,请你出来.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解初三学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的情况,并绘制成折线统计图(如图所示),那么关于该班45名同学一周参加体育锻炼时间的说法错误的是( )

A. 众数是9小时 B. 中位数是9 小时
C. 平均数是9小时 D. 锻炼时间不低于9小时的有14人
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) 48
 (
(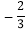 )- (-48)
)- (-48)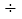 (-8) ;
(-8) ;(2) 12 〡0.5
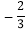 〡
〡 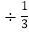 2 (3)2 ];
2 (3)2 ];(3)先化简,再求值:
已知m 3, n
 ,求3m2n 2mn2 2(mn
,求3m2n 2mn2 2(mn  m2n) mn] 3mn2 的值.
m2n) mn] 3mn2 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)
(1)如图①,画出⊙O的一个内接矩形;
(2)如图②,AB是⊙O的直径,CD是弦,且AB∥CD,画出⊙O的内接正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在八次数学测试中,甲、乙两人的成绩如下:
甲:89,93,88,91,94,90,88,87 乙:92,90,85,93,95,86,87,92
请你从下列角度比较两人成绩的情况,并说明理由:
(1)分别计算两人的极差;并说明谁的成绩变化范围大;
(2)根据平均数来判断两人的成绩谁优谁次;
(3)根据众数来判断两人的成绩谁优谁次;
(4)根据中位数来判断两人的成绩谁优谁次;
(5)根据方差来判断两人的成绩谁更稳定.
相关试题

