【题目】解方程:
(1)![]()
(2)![]() -
- ![]() =1
=1
参考答案:
【答案】
(1)解:去括号:2x+1-10x-1=6,
移项:2x-10x=6-1+1,
合并同类项:-8x=6,
系数化为1:x= ![]()
(2)解:去分母:4(2x-1)-3(5x+1)=24,
去括号,8x-4-15x-3=24,
移项,合并同类项:-7x=31,
系数化为1得:x=- ![]()
【解析】(1)先去括号,(括号前是负号,去掉括号和负号,括号里的每一项都要变号。)再移项合并同类项。然后将未知数的系数化为1,即可求解。
(2)先去分母(两边同时乘以24,右边的1也要乘以24,不能漏乘),再去括号(括号前是负号,去掉括号和负号,括号里的每一项都要变号。),然后移项合并同类项,最后把未知数的系数化为1,即可求解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本中有一个例题:
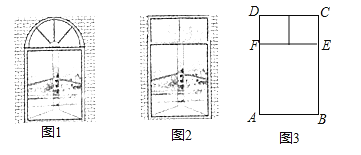
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,过AB边上的点D作GD∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD;

(1)求证:△ADG是等边三角形;
(2)求证:△AGE≌△DAC;
(3)过点E作EF∥DC,交BC于点F,连接AF,求∠AEF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
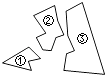
A.带①去
B.带②去
C.带③去
D.带①和②去 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=12cm,点E在AB上,且AE=
 AB,延长线段AB到点C,使BC=
AB,延长线段AB到点C,使BC=  AB,点D是BC的中点,求线段DE的长.
AB,点D是BC的中点,求线段DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,tanB=2。



(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF,求证:DF-EF=
 AF;
AF;(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论为____________。
-
科目: 来源: 题型:
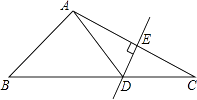
查看答案和解析>>【题目】如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
相关试题

