【题目】如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,tanB=2。



(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF,求证:DF-EF=![]() AF;
AF;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论为____________。
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)画图见解析,
①当EP在线段BC上时,有DFEF=![]() AF
AF
②当EP2BC时,DF+EF=![]() AF.
AF.
【解析】试题分析:(1)首先根据∠B的正切值知:AE=2BE,而E是BC的中点,结合平行四边形的对边相等即可得证.
(2)此题要通过构造全等三角形来求解;作GA⊥AF,交BD于G,通过证△AFE≌△AGD,来得到△AFG是等腰直角三角形且EF=GD,由此得证.
(3)辅助线作法和解法同(2),只不过结论有所不同而已.
试题解析:
(1)在Rt△ABE中,∠AEB=90°,
∴tanB=![]() =2,
=2,
∴AE=2BE。
∵E为BC的中点,
∴BC=2BE,
∴AE=BC。
∵ABCD是平行四边形,
∴AD=BC,
∴AE=AD。
(2)在DP上截取DH=EF(如图)
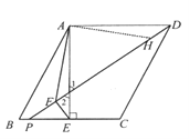
∵四边形ABCD是平行四边形,AE⊥BC,
∴∠EAD=90°。
∵EF⊥PD,∠l=∠2,
∴∠ADH=∠AEF。
∵AD=AE,
∴△ADH≌△AEF,
∴∠HAD=∠FAE,AH=AF,
∴∠FAH=90°。
在Rt△FAH中,AH=AF,
∴FH=![]() AF,
AF,
∴FH=FD-HD=FD-EF=![]() AF。
AF。
即DF-EF=![]() AF。
AF。
(3)按题目要求所画图形见图,
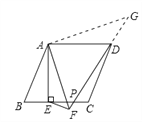
①当EP在线段BC上时,有DFEF=![]() AF
AF
②当EP2BC时,DF+EF=![]() AF.
AF.
③当EP>2BC时,EFDF=![]() AF.
AF.
点睛:此题主要考查的是平行四边形的性质以及全等三角形的判定和性质,难度适中,正确的构造出全等三角形是解答此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
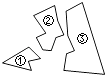
A.带①去
B.带②去
C.带③去
D.带①和②去 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)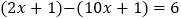
(2)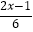 -
- 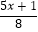 =1
=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=12cm,点E在AB上,且AE=
 AB,延长线段AB到点C,使BC=
AB,延长线段AB到点C,使BC=  AB,点D是BC的中点,求线段DE的长.
AB,点D是BC的中点,求线段DE的长.
-
科目: 来源: 题型:
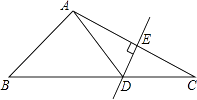
查看答案和解析>>【题目】如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化。从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果。所谓“老年人口抚养比”是指某范围人口中,老年人口数(65岁及以上人口数)与劳动年龄人口数(15-64岁人口数)之比,通常用百分比表示,用以表明每100名劳动年龄人口要负担多少名老年人。
以下是根据我国近几年的人口相关数据制作的统计图和统计表。
2011-2014年全国人口年龄分布图

2011-2014年全国人口年龄分布表
2011年
2012年
2013年
2014年
0-14岁人口占总人口的百分比
16.4%
16.5%
16.4%
16.5%
15-64岁人口占总人口的百分比
74.5%
74.1%
73.9%
73.5%
65岁及以上人口占总人口的百分比
m
9.4%
9.7%
10.0%
*以上图表中数据均为年末的数据。
根据以上材料解答下列问题:
(1)2011年末,我国总人口约为_______亿,全国人口年龄分布表中m的值为_______;
(2)若按目前我国的人口自然增长率推测,到2027年末我国约有14.60亿人。假设0-14岁人口占总人口的百分比一直稳定在16.5%,15-64岁的人口一直稳定在10亿,那么2027年末我国0-14岁人口约为_______亿,“老年人口抚养比”约为_______; (精确到1%)
(3)2016年1月1日起我国开始施行“全面二孩”政策,一对夫妻可生育两个孩子。在未来10年内,假设出生率显著提高,这_______(填“会”或“不会”)对我国的“老年人口抚养比”产生影响。
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂。”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少。
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树。他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约_______千米。
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米。小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:

考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值。
相关试题

