【题目】课本中有一个例题:
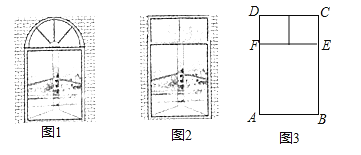
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
参考答案:
【答案】(1)![]() ;(2)与课本中的例题比较,现在窗户透光面积的最大值变大.
;(2)与课本中的例题比较,现在窗户透光面积的最大值变大.
【解析】(1)由已知可得:AD=![]() =
=![]() ,则S=1×
,则S=1×![]() =
=![]() ;
;
(2)设AB=x,则AD=![]() ,∵
,∵![]() >0,∴0<x<
>0,∴0<x<![]() ,设窗户面积为S,由已知得:S=ABAD=
,设窗户面积为S,由已知得:S=ABAD=![]() =
=![]() ,当x=
,当x=![]() 时,且x=
时,且x=![]() m在0<x<
m在0<x<![]() 的范围内,
的范围内,![]() =
=![]() >1.05,∴与课本中的例题比较,现在窗户透光面积的最大值变大.
>1.05,∴与课本中的例题比较,现在窗户透光面积的最大值变大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程
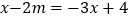 与
与 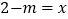 的解互为相反数,求
的解互为相反数,求 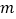 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具店购进一种儿童玩具,计划每个售价36元,能盈利80%,在销售中出现了滞销,于是先后两次降价,售价降为25元.
(1)求这种玩具的进价;
(2)求平均每次降价的百分率(精确到0.1%). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解中,正确的是( )
A.﹣2x3﹣3xy3+xy=﹣xy(2x2﹣3y2+1)
B.﹣y2﹣x2=﹣(y+x)(y﹣x)
C.16x2+4y2﹣16xy=4(2x﹣y)2
D.x2y+2xy+4y=y(x+2)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,过AB边上的点D作GD∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD;

(1)求证:△ADG是等边三角形;
(2)求证:△AGE≌△DAC;
(3)过点E作EF∥DC,交BC于点F,连接AF,求∠AEF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
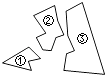
A.带①去
B.带②去
C.带③去
D.带①和②去 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)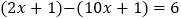
(2)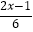 -
- 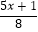 =1
=1
相关试题

