【题目】平面内的两条直线有相交和平行两种位置关系.
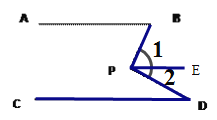
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
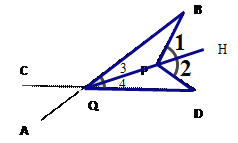
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
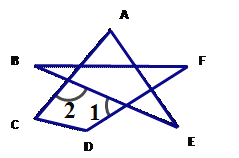
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

参考答案:
【答案】(1)不成立(2)∠BPD=∠BQD+∠B+∠D(3)∠A+∠B+∠C+∠D+∠E=180°
【解析】
【试题分析】(1)利用两直线平行,内错角相等,得:PE//AB,则![]() ;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则
;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则![]() ,利用等量代换得:∠BPD=
,利用等量代换得:∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
(2)利用三角形的外角等于不相邻的两个内角和,得![]() ,再利用角度转化即可.即
,再利用角度转化即可.即![]() =
=![]() .
.
(3)利用转化的思想,利用外角的性质,将6个角的和转化为四边形的内角和,即360°.
【试题解析】
(1)不成立,∠BPD=∠B+∠D.
理由:如图,作PE//AB,则![]() ,因为AB//CD,所以PE//CD,则
,因为AB//CD,所以PE//CD,则![]() ,所以∠BPD=
,所以∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
(2)作射线QP,![]() ,则
,则![]() =
=![]() .
.
即:![]() =
=![]() .
.
(3)由题意得:![]() ,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+
,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+![]() =360°.
=360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P1、P2是反比例函数y=
 (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点. 
(1)求反比例函数的解析式.
(2)①求P2的坐标. ②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y= 的函数值.
的函数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AD>AB.

(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲,乙两公司合作,12天可以完成;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,要使乙公司的总施工费较少,则甲公司每天的施工费应低于多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=135°,CD=6,AB=2,则四边形ABCD的面积为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为B1,B2,B3,B4,…,则B2018的坐标为________.

相关试题

