Question

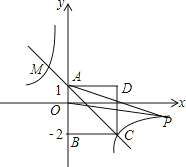
【题目】如图，四边形ABCD为正方形，点A的坐标为（0，1），点B的坐标为（0，﹣2），反比例函数y=的图象经过点C，一次函数y=ax+b的图象经过A、C两点.

（1）求反比例函数与一次函数的解析式;
（2）求反比例函数与一次函数的另一个交点M的坐标;
（3）若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标.

Answer 1

【答案】
（1）

解：（1）∵点A的坐标为（0，1），点B的坐标为（0，﹣2），

∴AB=1+2=3，

∵四边形ABCD为正方形，

∴Bc=3，

∴C（3，﹣2），

把C（3，﹣2）代入y=得k=3×（﹣2）=﹣6，

∴反比例函数解析式为y=﹣，

把C（3，﹣2），A（0，1）代入y=ax+b得，解得，

∴一次函数解析式为y=﹣x+1

（2）

解：解方程组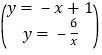得或，

∴M点的坐标为（﹣2，3）；

（3）

解：

设P（t，﹣），

∵△OAP的面积恰好等于正方形ABCD的面积，

∴×1×|t|=3×3，解得t=18或t=﹣18，

∴P点坐标为（18，﹣）或（﹣18，）

【解析】（1）先根据A点和B点坐标得到正方形的边长，则BC=3，于是可得到C（3，﹣2），然后利用待定系数法求反比例函数与一次函数的解析式；
（2）通过解关于反比例函数解析式与一次函数的解析式所组成的方程组可得到M点的坐标；
（3）设P（t，﹣），根据三角形面积公式和正方形面积公式得到×1×|t|=3×3，然后解绝对值方程求出t即可得到P点坐标．