【题目】如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(﹣2,0)、B(4,0),其顶点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)设P点的坐标为(x,y),△PBE的面积为S,求S与x之间的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取值最大值时,过点P作x轴的垂线,垂足为F,连接EF,△PEF沿直线EF折叠,点P的对应点为点P′,请直接写出P′点的坐标,并判断点P′是否在该抛物线上.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+bx+4(a≠0)经过A(﹣2,0)、B(4,0)两点
∴把(﹣2,0)、B(4,0)代入抛物线得:a=﹣![]() ,b=1,
,b=1,
∴抛物线解析式为:y=﹣![]() x2+x+4.
x2+x+4.
∴顶点D的坐标为(1,![]() );
);
(2)
解:设直线BD解析式为:y=kx+b(k≠0),把B、D两点坐标代入,
得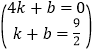 ,
,
解得k=﹣![]() ,b=6,
,b=6,
直线BD解析式为y=﹣![]() x+6,
x+6,
S=![]() PEOE,
PEOE,
S=![]() PEOE=
PEOE=![]() xy=
xy=![]() x(﹣
x(﹣![]() x+6)=﹣
x+6)=﹣![]() x2+3x,
x2+3x,
∵顶点D的坐标为(1,![]() ),B(4,0)
),B(4,0)
∴1<x<4,
∴S=﹣![]() x2+3x(1<x<4),
x2+3x(1<x<4),
S=﹣![]() (x2﹣4x++4)+3,
(x2﹣4x++4)+3,
=﹣![]() (x﹣2)2+3,
(x﹣2)2+3,
∴当x=2时,S取得最大值,最大值为3.
(3)
解:当S取得最大值,x=2,y=3,
∴P(2,3),
∴四边形PEOF是矩形.
作点P关于直线EF的对称点P′,连接P′E,P′F.
过P′作P′H⊥y轴于H,P′F交y轴于点M,
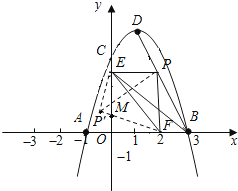
设MC=m,则MF=m,P′M=3﹣m,P′E=2,
在Rt△P′MC中,由勾股定理,
22+(3﹣m)2=m2,
解得m=![]() ,
,
∵CMP′H=P′MP′E,
∴P′H=![]() ,
,
由△EHP′∽△EP′M,
可得![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:EH=![]() .
.
∴OH=3﹣![]() =
=![]() .
.
∴P′坐标(﹣![]() ,
,![]() ).不在抛物线上.
).不在抛物线上.
【解析】(1)本题需先根据抛物线y=ax2+bx+4(a≠0)经过A(﹣2,0)、B(4,0)两点,分别求出a、b的值,再代入抛物线y=ax2+bx+4即可求出它的解析式.
(2)本题首先设出BD解析式y=kx+b,再把B、D两点坐标代入求出k、b的值,得出BD解析式,再根据面积公式即可求出最大值.
(3)本题需先根据(2)得出最大值来,求出点P的坐标,得出四边形PEOF是矩形,再作点P关于直线EF的对称点P′设出MC=m,则MF=m.从而得出P′M与P′E的值,根据勾股定理,得出m的值,再由△EHP′∽△EP′M,得出EH和OH的值,最后求出P′的坐标,判断出不在抛物线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE.

(1)求证:EC=DA;
(2)若AC⊥CB,试判断四边形AECD的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,﹣2),反比例函数y=
 的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是
 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
(1)求证:AC=CD;
(2)若OC= ,求BH的长.
,求BH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( )

A.43
B.45
C.51
D.53 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )

A.18 ﹣9π
﹣9π
B.18﹣3π
C.9 ﹣
﹣ 
D.18 ﹣3π
﹣3π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:
 ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据: 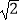 ≈1.41,
≈1.41,  ≈1.73,
≈1.73, 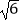 ≈2.45)
≈2.45)
A.30.6
B.32.1
C.37.9
D.39.4
相关试题

