【题目】已知⊙O的直径AB=4,点C在⊙O上,连接AC,沿AC折叠劣弧![]() ,记折叠后的劣弧为
,记折叠后的劣弧为![]() .
.
(1)如图1,当![]() 经过圆心O时,求
经过圆心O时,求![]() 的长.
的长.
(2)如图2,当![]() 与AB相切于A时.
与AB相切于A时.
①画出![]() 所在的圆的圆心P.
所在的圆的圆心P.
②求出阴影部分弓形![]() 的面积.
的面积.


参考答案:
【答案】(1)![]() ;(2)π﹣2.
;(2)π﹣2.
【解析】
(1)只要证明△EA O是等边三角形即可解决问题;
(2)①过A点作AP⊥AB,再截取AP=2,则P点为所求,如图2;
②只要证明四边形AOCP是正方形即可解决问题.
(1)作半径OE⊥AC于F,连接AE,如图1,
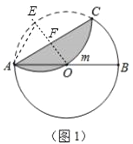
∵沿AC折叠劣弧![]() ,记折叠后的劣弧为
,记折叠后的劣弧为![]() ,
,
∴OF=![]() OE=OF,
OE=OF,
∵OE⊥AC,
∴AE=AO,
∵OA=OE,
∴AE=AO=OE,
∴△AOE是等边三角形,
∴∠AEO=60°,
∴![]() 的长=
的长=![]() ;
;
(2)①过A点作AP⊥AB,再截取AP=2,则P点为所求,如图2;
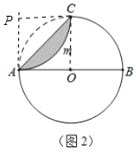
②连结PC、OC,
∵AP=OA=OC=PC=2,
∴四边形PAOC为菱形,
而∠PAO=90°,
∴四边形PAOC为正方形,
∴S阴=![]() ×2×2=π﹣2.
×2×2=π﹣2.
-
科目: 来源: 题型:
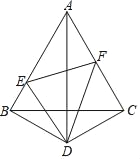
查看答案和解析>>【题目】如图所示,D是等边三角形ABC外一点,DB=DC,∠BDC=120°,点E,F分别在AB,AC上.
(1)求证:AD是BC的垂直平分线.
(2)若ED平分∠BEF,求证:FD平分∠EFC.
(3)在(2)的条件下,求∠EDF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:
 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C为线段AB上一点,△ACM、△BCN是等边三角形.
(1)如图1,求证:AN=BM;
(2)如图2,将△ACM绕点C按逆时针方向旋转180°,使点A落在CB上,结论“AN=BM”是否还成立,若成立,请证明:若不成立,请说明理由;
(3)在(2)所得的图形中,设MA的延长线交BN于D(如图3),试判断△ABD的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点O,∠BAC=80°,则∠BOC的度数是( )

A.130°B.120°C.100°D.90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据对徐州市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数
 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数 的图象如图②所示.
的图象如图②所示.
(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时 获得的销售利润之和最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )

A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
相关试题

