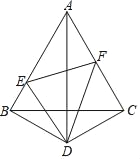
【题目】如图所示,D是等边三角形ABC外一点,DB=DC,∠BDC=120°,点E,F分别在AB,AC上.
(1)求证:AD是BC的垂直平分线.
(2)若ED平分∠BEF,求证:FD平分∠EFC.
(3)在(2)的条件下,求∠EDF的度数.
参考答案:
【答案】(1)见解析;(2)见解析;(3)∠EDF=60°.
【解析】
(1)求出AB=AC,BD=DC,根据线段垂直平分线性质求出即可;
(2)过D作DM⊥EF,连接AD,求出AD平分∠BAC,求出∠ABC=∠ACB=60°,求出BD=DM,BD=DC,推出DM=DC即可;
(3)求出DB=DM,DM=DC,∠EBD=∠EMD=90°,证出△EBD≌△EMD,推出∠BDE=∠EDM,同理∠CDF=∠FDM,进而得出2∠EDF=∠BDC=120°.
(1)∵△ABC是等边三角形,
∴AB=AC,
∴A在BC的垂直平分线上,
∵BD=DC,
∴D在BC的垂直平分线上,
∴AD是BC的垂直平分线
(2)过D作DM⊥EF,连接AD,
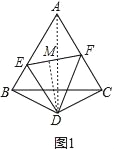
∵AD是BC的垂直平分线,
∴AD平分∠BAC,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD=DC,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴DB⊥AB,DC⊥AC,
∵DM⊥EF,ED平分∠BEF,AD平分∠BAC,
∴BD=DM,BD=DC,
∴DM=DC,
∴FD平分∠EFC;
(3)如图,
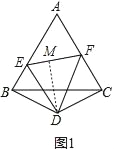
∵DE平分∠BEF,DB⊥AB,DM⊥EF,DF平分∠CFE,
∴DB=DM,DM=DC,∠EBD=∠EMD=90°,
在△EBD和△EMD中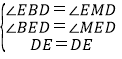 ,
,
∴△EBD≌△EMD,
∴∠BDE=∠EDM,
同理∠CDF=∠FDM,
∴2∠EDF=∠BDC=180°﹣30°﹣30°=120°,
∴∠EDF=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地有两条公路:一条是全长400千米的普通公路,一条是全长360千米的高速公路.某客车在高速公路上行驶的平均速度比在普通公路上行驶的平均速度快50千米/时,从甲地到乙地由高速公路上行驶所需的时间比普通公路上行驶所需的时间少6小时.求该客车在高速公路上行驶的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF

(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对“A:古诗词,B:国画,C:京剧,D:书法”等中国传统文化项目的最喜爱情况,在全校范围内随机抽取部分学生进行问卷调查(每人限选一项),并将调查结果绘制成如下不完整的统计图.
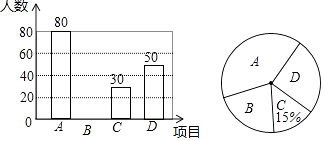
请结合统计图回答下列问题:
(1)在这次调查中,一共调查了名学生;在扇形统计图中,项目B对应扇形的圆心角是度;
(2)如果该校共有2000名学生,请估计该校最喜爱项目A的学生有多少人?
(3)若该校在A、B、C、D四项中任选两项成立课外兴趣小组,请用画树状图(或列表)计算恰好选中项目A和D的概率.
故答案为:200,72; -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划从本地向甲、乙两地运送海产品进行销售.本地与甲、乙两地都有铁路和公路相连(如图所示),铁路的单位运价为2元/(吨千米),公路的单位运价为3元/(吨千米)
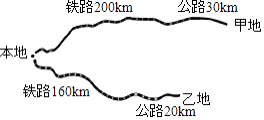
(1)若公司计划往甲、乙两地运输海产品共需铁路运费3680元,公路运费780元,求计划从本地向甲乙两地运输海产品各多少吨?
(2)经市场调查发现,甲地海产品的实际需求量比计划减少a(a>0)吨,但运到甲、乙两地的总量不变,且运到甲地的海产品不少于运到乙地的海产品,当a为多少时,实际总运费w最低?最低总运费是多少? (参考公式:货运运费=单位运价×运输里程×货物重量) -
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
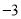
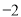

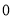
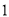
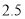
筐 数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价
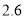 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元?
相关试题

