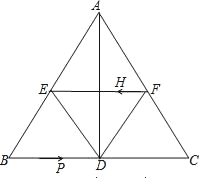
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
参考答案:
【答案】(1)证明见解析;(2)20;(3)2秒
【解析】试题分析:(1)根据等腰三角形的三线合一可得出D为BC的中点,结合E、F分别为AB、AC的中点可得出DE和DF是△ABC的中位线,根据中位线的定义可得出DE∥AC、DF∥AB,即四边形AEDF是平行四边形,根据三角形中位线定义可得出DE=![]() AC、DF=
AC、DF=![]() AB,结合AB=AC即可得出DE=DF,从而得出四边形AEDF是菱形;
AB,结合AB=AC即可得出DE=DF,从而得出四边形AEDF是菱形;
(2)根据中位线的定义可得出EF的长度,根据菱形的面积公式可求出菱形AEDF的面积;
(3)由中位线的定义可得出EF∥BC,根据平行四边形的判定定理可得出关于t的一元一次方程,解之即可得出结论.
详解:(1)证明:∵AB=AC,AD⊥BC,
∴D为BC的中点.
∵E、F分别为AB、AC的中点,
∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF,
∴四边形AEDF是菱形,
(2)解:∵EF为△ABC的中位线,
∴EF=![]() BC=5.
BC=5.
∵AD=8,AD⊥EF,
∴S菱形AEDF=![]() ADEF=
ADEF=![]() ×8×5=20.
×8×5=20.
(3)解:∵EF∥BC,
∴EH∥BP.
若四边形BPHE为平行四边形,则须EH=BP,
∴5﹣2t=3t,
解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形.
∵EF∥BC,
∴FH∥PC.
若四边形PCFH为平行四边形,则须FH=PC,
∴2t=10﹣3t,
解得:t=2,
∴当t=2秒时,四边形PCFH为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
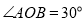 ,点
,点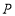 为
为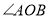 内一点,
内一点,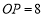 ,点
,点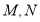 分别在射线
分别在射线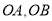 上,当
上,当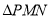 的周长最小时,下列结论:①
的周长最小时,下列结论:①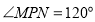 ;②
;②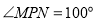 ;③
;③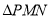 的周长最小值为24;④
的周长最小值为24;④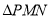 的周长最小值为8;其中正确的序号为__________.
的周长最小值为8;其中正确的序号为__________.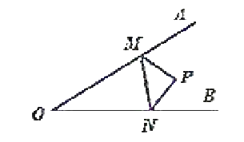
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,M,N分别是AD,BC的中点,E,F分别是线段BM,CM的中点,若AB=8,AD=12,则四边形ENFM的周长是多少?
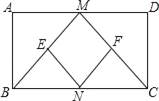
-
科目: 来源: 题型:
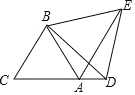
查看答案和解析>>【题目】如图,
 是边长为2的等边三角形,
是边长为2的等边三角形, 是
是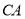 延长线上一点,以
延长线上一点,以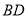 为边作等边三角形
为边作等边三角形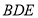 ,连接
,连接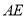 .
.
(1)求
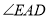 的度数.
的度数.(2)求
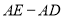 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在
 轴上,记为
轴上,记为 ,折痕为CE.直线CE的关系式是
,折痕为CE.直线CE的关系式是 ,与
,与 轴相交于点F,且AE=3.
轴相交于点F,且AE=3.(1)求OC长度;
(2)求点
 的坐标;
的坐标;(3)求矩形ABCO的面积.

相关试题

