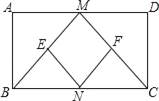
【题目】如图,在矩形ABCD中,M,N分别是AD,BC的中点,E,F分别是线段BM,CM的中点,若AB=8,AD=12,则四边形ENFM的周长是多少?
参考答案:
【答案】20
【解析】分析:根据M是边AD的中点,得AM=DM=6,根据勾股定理得出BM=CM=10,再根据E、F分别是线段BM、CM的中点,即可得出EM=FM=5,再根据N是边BC的中点,得出EM=FN,EN=FM,从而得出四边形ENFM的周长.
详解:∵M、N分别是边AD、BC的中点,AB=8,AD=12,
∴AM=DM=6,
∵四边形ABCD为矩形,
∴∠A=∠D=90°,
∴BM=CM=10,
∵E、F分别是线段BM、CM的中点,
∴EM=FM=5,
∴EN,FN都是△BCM的中位线,
∴EN=FN=5,
∴四边形ENFM的周长为5+5+5+5=20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
-
科目: 来源: 题型:
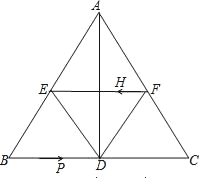
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是边长为2的等边三角形,
是边长为2的等边三角形, 是
是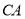 延长线上一点,以
延长线上一点,以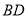 为边作等边三角形
为边作等边三角形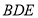 ,连接
,连接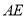 .
.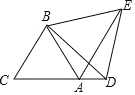
(1)求
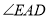 的度数.
的度数.(2)求
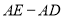 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在
 轴上,记为
轴上,记为 ,折痕为CE.直线CE的关系式是
,折痕为CE.直线CE的关系式是 ,与
,与 轴相交于点F,且AE=3.
轴相交于点F,且AE=3.(1)求OC长度;
(2)求点
 的坐标;
的坐标;(3)求矩形ABCO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段a和线段AB ( a <AB).
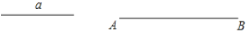
(1)以AB为一边,画△ABC ,使AC a , A=50 ,用直尺、圆规作出△ABC边BC的垂直平分线,分别与边AB、BC 交于点D、E,联结CD ;(不写画法,保留作图痕迹)
(2)在(1)中,如果AB5 ,AC3 ,那么△ADC 的周长等于 .
相关试题

