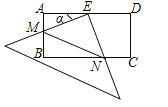
【题目】在矩形ABCD中，AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N，设∠AEM=α（0°＜α＜90°），给出下列四个结论：

①AM=CN；②∠AME=∠BNE；③BN﹣AM=2；④S△EMN=．

上述结论中正确的个数是（ ）

A．1 B．2 C．3 D．4

参考答案：

【答案】C．

【解析】

试题分析：①如图，在矩形ABCD中，AD=2AB，E是AD的中点，作EF⊥BC于点F，则有AB=AE=EF=FC，∵∠AEM+∠DEN=90°，∠FEN+∠DEN=90°，∴∠AEM=∠FEN，在Rt△AME和Rt△FNE中，∵∠AEM=∠FEN，AE=EF，∠MAE=∠NFE，∴Rt△AME≌Rt△FNE，∴AM=FN，∴MB=CN．

∵AM不一定等于CN，∴AM不一定等于CN，∴①错误，②由①有Rt△AME≌Rt△FNE，∴∠AME=∠BNE，∴②正确，③由①得，BM=CN，∵AD=2AB=4，∴BC=4，AB=2

∴BN﹣AM=BC﹣CN﹣AM=BC﹣BM﹣AM=BC﹣（BM+AM）=BC﹣AB=4﹣2=2，∴③正确，④如图，

由①得，CN=CF﹣FN=2﹣AM，AE=AD=2，AM=FN

∵tanα=，∴AM=AEtanα

∵cosα==，∴ ，∴=1+=1+=1+，∴=2（1+）

∴S△EMN=S四边形ABNE﹣S△AME﹣S△MBN

=（AE+BN）×AB﹣AE×AM﹣BN×BM

=（AE+BC﹣CN）×2﹣AE×AM﹣（BC﹣CN）×CN

=（AE+BC﹣CF+FN）×2﹣AE×AM﹣（BC﹣2+AM）（2﹣AM）

=AE+BC﹣CF+AM﹣AE×AM﹣（2+AM）（2﹣AM）

=AE+AM﹣AE×AM+

=AE+AEtanα﹣tanα+

=2+2tanα﹣2tanα+2

=2（1+）

=，∴④正确．

故选C．

关闭