【题目】在平面直角坐标系中,OA=4,OC=8,四边形ABCO是平行四边形.
(1)求点B的坐标及四边形ABCO的面积;
(2)若点P从点C以2单位长度/秒的速度沿CO方向移动,同时点Q从点O以1单位长度/秒的速度沿OA方向移动,设移动的时间为t秒,△AQB与△BPC的面积分别记为![]() ,
,![]() ,四边形QBPO的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.
,四边形QBPO的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.
(3)在(2)的条件下,是否存在某个时同,使![]() ,若存在,求出t的值,若不存在,试说明理由;
,若存在,求出t的值,若不存在,试说明理由;

参考答案:
【答案】(1)点B的坐标为(8,4),四边形ABCO的面积32;(2)四边形QBPO的面积不发生变化,面积为定值16,证明过程见解析;(3)存在t的值,此时![]() .
.
【解析】
(1)先证四边形ABCO是矩形,进而可根据OA=4,OC=8求得答案;
(2)由题意可知OQ=t,CP=2t,进而可用含t的代数式表示S△ABQ及S△BCP,进而可根据 S四边形QBPO=S矩形ABCO- S△ABQ- S△BCP=32-(16-4t)-4t,化简即可得到答案;
(3)由(2)可知:S△ABQ=16-4t,S四边形QBPO=16,再结合![]() 即可求得t的值.
即可求得t的值.
解:(1)∵四边形ABCO是平行四边形,∠AOC=90°,
∴四边形ABCO是矩形,
∵OA=4,OC=8,
∴点B的坐标为(8,4),S矩形ABCO=OA·OC=8×4=32,
(2)∵四边形ABCO是矩形,
∴AB=OC=8,BC=OA=4,
由题意可知:OQ=t,CP=2t,
∴AQ=OA-OQ=4-t,
∴S△ABQ=![]() AB·AQ=
AB·AQ=![]() ×8(4-t)=16-4t,
×8(4-t)=16-4t,
S△BCP=![]() BC·CP=
BC·CP=![]() ×4×2t=4t,
×4×2t=4t,
∴S四边形QBPO=S矩形ABCO-S△ABQ-S△BCP
=32-(16-4t)-4t
=32-16+4t-4t
=16,
∴四边形QBPO的面积不变,面积为16;
(3)由(2)可知:S△ABQ=16-4t,S四边形QBPO=16,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴存在t的值使得![]() ,此时
,此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.

⑴写出A′、B′、C′的坐标;
⑵求出△ABC的面积;
⑶点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一场活动中活动主办方为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两纪念品发放其中甲种纪念品每件售价120元,乙种纪念品每件售价80元,
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
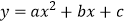 的图像与
的图像与 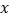 轴交于点
轴交于点 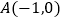 、
、 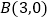 ,与
,与 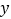 轴交于点
轴交于点 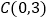 .
.
(1)求二次函数的表达式;
(2)设上述抛物线的对称轴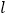 与
与 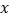 轴交于点
轴交于点 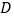 ,过点
,过点 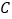 作
作 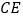 ⊥
⊥ 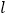 于
于 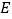 ,
, 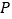 为线段
为线段 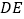
上一点,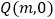 为
为 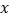 轴负半轴上一点,以
轴负半轴上一点,以 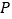 、
、 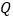 、
、 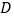 为顶点的三角形与
为顶点的三角形与 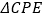 相似;
相似;
满足条件的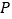 点有且只有一个时,求
点有且只有一个时,求 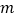 的取值范围;
的取值范围;
②若满足条件的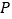 点有且只有两个,直接写出
点有且只有两个,直接写出 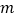 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E是边CD的中点,连接BE并延长,交AD延长线于点F,连接BD、CF.
(1)求证:△CEB≌△DEF;
(2)若AB=BF,试判断四边形BCFD的形状,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买100个A型放大镜和150个B型放大镜需用1500元;若购买120个A型放大镜和160个B型放大镜需用1720元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)学校决定购买A型放大镜和B型放大镜共75个,总费用不超过570元,那么最多可以购买多少个A型放大镜?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

相关试题

