【题目】一场活动中活动主办方为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两纪念品发放其中甲种纪念品每件售价120元,乙种纪念品每件售价80元,
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
参考答案:
【答案】(1)甲种纪念品购买了40件,乙种纪念品购买了60件;(2)共有两种方案,分别为方案一:购买甲种纪念品34件,乙种纪念品66件;方案二:购买甲种纪念品35件,乙种纪念品65件,其中方案一所需总费用最少,最少总费用是9360元.
【解析】
(1)设甲种纪念品购买了x件,乙种纪念品购买了(100﹣x)件,利用购买甲、乙两种纪念品一共花费了9600元列方程120x+80(100﹣x)=9600,然后解方程求出x,再计算(100﹣x)即可;
(2)设购买甲种纪念品m件,乙种奖品购买了(100﹣m)件,利用购买乙种纪念品的件数不超过甲种奖品件数的2倍,总花费不超过9400元列不等式组,然后解不等式组后确定x的整数值即可得到组委会的购买方案.
解:(1)设甲种纪念品购买了x件,乙种纪念品购买了(100﹣x)件,
根据题意得120x+80(100﹣x)=9600,
解得x=40,
则100﹣x=60,
答:甲种纪念品购买了40件,乙种纪念品购买了60件;
(2)设购买甲种纪念品m件,乙种奖品购买了(100﹣m)件,
根据题意,得 ![]() ,
,
解得 ![]() ≤m≤35,
≤m≤35,
∵m为整数,
∴m=34或m=35,
方案一:当m=34时,100﹣m=66,费用为:34×120+66×80=9360(元)
方案二:当m=35时,100﹣m=65,费用为:35×120+65×80=9400(元)
由于9400>9360,
所以方案一的费用低,费用为9360元.
答:共有两种方案,分别为方案一:购买甲种纪念品34件,乙种纪念品66件;方案二:购买甲种纪念品35件,乙种纪念品65件,其中方案一所需总费用最少,最少总费用是9360元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

-
科目: 来源: 题型:
查看答案和解析>>【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
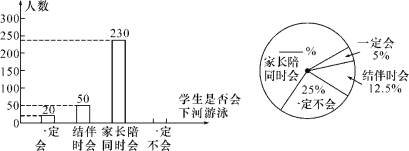
(1)这次抽样调查中,共调查了__ __名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.

⑴写出A′、B′、C′的坐标;
⑵求出△ABC的面积;
⑶点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
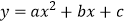 的图像与
的图像与 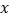 轴交于点
轴交于点 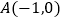 、
、 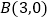 ,与
,与 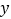 轴交于点
轴交于点 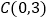 .
.
(1)求二次函数的表达式;
(2)设上述抛物线的对称轴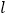 与
与 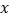 轴交于点
轴交于点 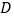 ,过点
,过点 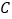 作
作 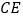 ⊥
⊥ 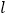 于
于 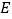 ,
, 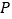 为线段
为线段 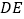
上一点,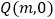 为
为 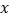 轴负半轴上一点,以
轴负半轴上一点,以 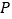 、
、 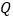 、
、 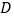 为顶点的三角形与
为顶点的三角形与 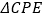 相似;
相似;
满足条件的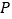 点有且只有一个时,求
点有且只有一个时,求 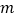 的取值范围;
的取值范围;
②若满足条件的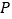 点有且只有两个,直接写出
点有且只有两个,直接写出 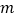 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,OA=4,OC=8,四边形ABCO是平行四边形.
(1)求点B的坐标及四边形ABCO的面积;
(2)若点P从点C以2单位长度/秒的速度沿CO方向移动,同时点Q从点O以1单位长度/秒的速度沿OA方向移动,设移动的时间为t秒,△AQB与△BPC的面积分别记为
 ,
, ,四边形QBPO的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.
,四边形QBPO的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.(3)在(2)的条件下,是否存在某个时同,使
 ,若存在,求出t的值,若不存在,试说明理由;
,若存在,求出t的值,若不存在,试说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E是边CD的中点,连接BE并延长,交AD延长线于点F,连接BD、CF.
(1)求证:△CEB≌△DEF;
(2)若AB=BF,试判断四边形BCFD的形状,并证明.

相关试题

