【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
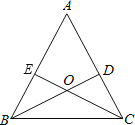
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
参考答案:
【答案】(1)证明见解析(2)点O在∠BAC的角平分线上,理由见解析
【解析】
试题分析:(1)由OB=OC,即可求得∠OBC=∠OCB,又由,锐角△ABC的两条高BD、CE相交于点O,根据三角形的内角和等于180°,即可证得△ABC是等腰三角形;
(2)首先连接AO并延长交BC于F,通过证△AOB≌△AOC(SSS),得到∠BAF=∠CAF,即点O在∠BAC的角平分线上.
(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠CDB=90°,
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°﹣∠BEC﹣∠BCE=180°﹣∠CDB﹣∠CBD,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
(2)解:点O在∠BAC的角平分线上.
理由:连接AO并延长交BC于F,
在△AOB和△AOC中,
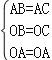
∴△AOB≌△AOC(SSS).
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,且
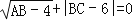 ,点P、Q分别是边AD、AB上的动点.
,点P、Q分别是边AD、AB上的动点.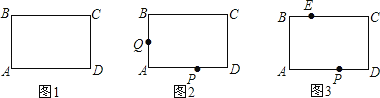
(1)求BD的长;
(2)①如图2,在P、Q运动中是否能使△CPQ成为等腰直角三角形?若能,请求出PA的长;若不能,请说明理由;
②如图3,在BC上取一点E,使EC=5,那么当△EPC为等腰三角形时,求出PA的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若α、β是一元二次方程x2+2x﹣6=0的两根,则α2+β2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a5÷a3=a2 B. a3+a3=a6 C. (a3)2=a5 D. a5·a3=2a8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
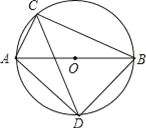
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=kx2﹣2kx﹣3k交x轴于A、B两点,交y轴于点C,已知OC=OB.
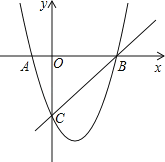
(1)求抛物线解析式;
(2)在直线BC上求点P,使PA+PO的值最小;
(3)抛物线上是否存在点Q,使△QBC的面积等于6?若存在,请求出Q的坐标;若不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AD=8,
 ABC=1200,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为_________.
ABC=1200,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为_________.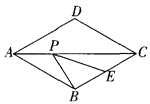
相关试题

