【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
参考答案:
【答案】(1)30秒;(2)0.6秒;(3)![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)设两车经过x秒相遇,根据相遇时,两车行驶的路程之和等于隧道的长列出方程,解方程即可;
(2)设两车从相遇到完全离开所需的时间为y秒,等量关系为:速度和×时间=两车的车长之和,依此列出方程,解方程即可;
(3)先根据小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍,求出两车相遇后一共行驶的路程之和,再除以速度和即可.分两种情况进行讨论:①车尾相遇前;②车尾相遇后.
(1)设两车经过x秒相遇,根据题意得:
(10+30)x=1200
解得:x=30.
答:两车经过30秒相遇;
(2)设两车从相遇到完全离开所需的时间为y秒,根据题意得:
(10+30)y=4+20
解得:y=0.6.
答:两车从相遇到完全离开所需的时间为0.6秒;
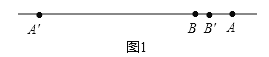
(3)设AB表示车长为4米的小轿车,其中点A表示车头,点B表示车尾,A'B'表示车长为20米的大货车,其中点A'表示车头,点B'表示车尾,则AB=4米,A'B'=20米,设BB'=a米.
分两种情况:①车尾相遇前,如图1,则AB'=(4﹣a)米.
小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时,AA'=4BB',所以20+4﹣a=4a,解得:a![]() ,则AA'
,则AA'![]() ,故所求时间为:
,故所求时间为:![]() (10+30)
(10+30)![]() (秒);
(秒);
②车尾相遇后,如图2,则AB'=(4+a)米.
小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时,AA'=4BB',所以20+4+a=4a,解得:a=8,则AA'=32,故所求时间为:32÷(10+30)![]() (秒).
(秒).

综上所述:当小轿车车头和大货车车头相遇后,小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间为![]() 秒或
秒或![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).
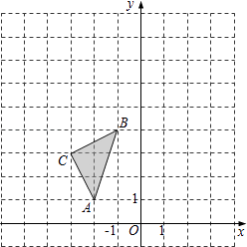
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出A1点的坐标及sin∠B1A1C1的值;
以原点O为位似中心,位似比为1:2,在y轴的左侧,画出 将△ABC放大后的△A2B2C2 , 并写出A2点的坐标;
(2)若点D(a,b)在线段AB上,直接写出经过(2)的变化后点D的对应点D2的坐标. -
科目: 来源: 题型:
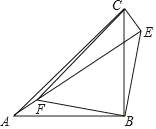
查看答案和解析>>【题目】如图,点E是等腰三角形纸片ABC外一点,∠ABC=90°,连接AE,点F是线段AE(不与点A,E重合)上一点,在△EBF中,EB=FB,∠EBF=90°,连接CE,CF
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
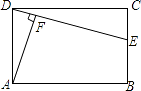
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程4x2+4(a﹣1)x+a2﹣a﹣2=0没有实数根.
(1)求实数a的取值范围;
(2)化简: ﹣
﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有四个分别标有数字﹣2,﹣1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为b.
(1)用列表法或画树状图表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数y=x2的图象上的概率;
(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过一、二、三象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少千米?
(2)他中途休息了多长时间?
(3)他从休息后直达目的地这段时间的速度是多少?(列式计算)

相关试题

