【题目】在一个不透明的盒子里,装有四个分别标有数字﹣2,﹣1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为b.
(1)用列表法或画树状图表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数y=x2的图象上的概率;
(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过一、二、三象限的概率.
参考答案:
【答案】
(1)解:画树状图如下:
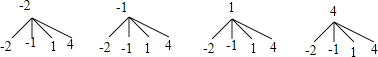
共有16种等可能的结果,它们为(﹣2,﹣2)、(﹣2,﹣1)、(﹣2,1)、(﹣2,4)、(﹣1,﹣2)、(﹣1,﹣1)、(﹣1,1)、(﹣1,4)、(1,﹣2)、(1,﹣1)、(1,1)、(1,4)、(4,﹣2)、(4,﹣1)、(4,1)、(4,4)
(2)解:落在二次函数y=x2的图象上的点有(﹣2,4),(﹣1,1),(1,1),
所以落在二次函数y=x2的图象上的概率= ![]() ;
;
(3)解:满足直线y=ax+b经过一、二、三象限的点有(1,1),(1,4),(4,1),(4,4),
所以满足直线y=ax+b经过一、二、三象限的概率= ![]() =
= ![]()
【解析】(1)根据题意列出树状图知共有16种等可能的结果,它们为(﹣2,﹣2)、(﹣2,﹣1)、(﹣2,1)、(﹣2,4)、(﹣1,﹣2)、(﹣1,﹣1)、(﹣1,1)、(﹣1,4)、(1,﹣2)、(1,﹣1)、(1,1)、(1,4)、(4,﹣2)、(4,﹣1)、(4,1)、(4,4);
(2)由(1)知共有16种等可能的结果,落在二次函数y=x2的图象上的点有3种,根据概率公式计算即可;
(3)由(1)知共有16种等可能的结果,满足直线y=ax+b经过一、二、三象限的点有4种,根据概率公式计算即可。
【考点精析】本题主要考查了列表法与树状图法和概率公式的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
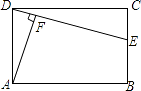
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程4x2+4(a﹣1)x+a2﹣a﹣2=0没有实数根.
(1)求实数a的取值范围;
(2)化简: ﹣
﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少千米?
(2)他中途休息了多长时间?
(3)他从休息后直达目的地这段时间的速度是多少?(列式计算)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。

证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:
 (即AB:BC=1:
(即AB:BC=1:  ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
相关试题

