【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).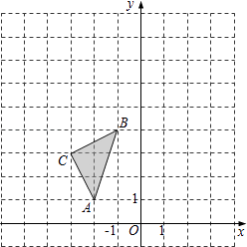
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出A1点的坐标及sin∠B1A1C1的值;
以原点O为位似中心,位似比为1:2,在y轴的左侧,画出 将△ABC放大后的△A2B2C2 , 并写出A2点的坐标;
(2)若点D(a,b)在线段AB上,直接写出经过(2)的变化后点D的对应点D2的坐标.
参考答案:
【答案】
(1)解:如图,△A1B1C1,△A2B2C2,即为所求,
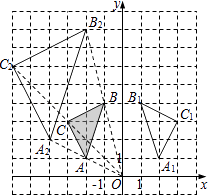
①A1(2,1),
∵ ![]() =B1C
=B1C ![]() +A1C
+A1C ![]() ,A1C1=B1C1,
,A1C1=B1C1,
∴△A1B1C1是等腰直角三角形,
∴sin∠B1A1C1=sin45°= ![]() ;
;
②A2(﹣4,2)
(2)解:∵点D(a,b)在线段AB上,位似比为1:2,
∴D2(2a,2b)
【解析】(1)利用关于y轴对称的点的坐标特点得出A,B,C对应点的坐标,在坐标平面内描出这些点,再顺次连接即可;根据方格纸的特点利用勾股定理计算出△A1B1C1三边的长,根据勾股定理得逆定理得出△A1B1C1是等腰直角三角形,,然后利用sin∠B1A1C1=sin45°得出答案;根据位似图形的性质,连接OA并延长至点A2,使OA=OA2,同理作出B2,C2,再顺次连接即可;根据图形写出A1,A2
(2)利用位似比得出对应点的坐标变化规律进而得出答案。
【考点精析】本题主要考查了作轴对称图形和位似变换的相关知识点,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线;它们具有相似图形的性质外还有图形的位置关系(每组对应点所在的直线都经过同一个点—位似中心)才能正确解答此题.
-
科目: 来源: 题型:
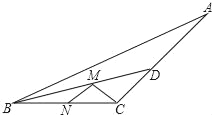
查看答案和解析>>【题目】如图,钝角三角形△ABC的面积是15,最长边AB=10,BD平分∠ABC,点M,N分别是BD,BC上的动点,则CM+MN的最小值为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 ﹣4
﹣4  ﹣tan60°+|
﹣tan60°+|  ﹣2|.
﹣2|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,∠ACB=90°,AC=3
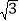 ,BC=3,如图②,将△ABC沿一条直线折叠,使得点A与点C重合
,BC=3,如图②,将△ABC沿一条直线折叠,使得点A与点C重合(1)在图①中画出折痕所在的直线l,设直线l与AB,AC分别相交于点D,E(尺规作图,不写作法,保留作图痕迹)
(2)如图②,求△CDB的周长.
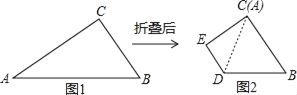
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是等腰三角形纸片ABC外一点,∠ABC=90°,连接AE,点F是线段AE(不与点A,E重合)上一点,在△EBF中,EB=FB,∠EBF=90°,连接CE,CF
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
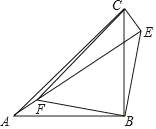
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
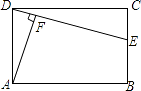
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
相关试题

