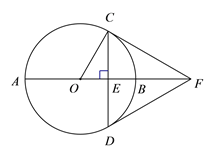
【题目】如图,![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]()
![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接DF.
,连接DF.
(1)求证:DF是⊙![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() =30°,
=30°,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】(1) 连接OD,由垂径定理证OF为CD的垂直平分线,得CF=DF,∠CDF=∠DCF,由∠CDO=∠OCD,再证∠CDO +∠CDB=∠OCD+∠DCF=90°,可得OD⊥DF,结论成立.
(2) 由∠OCF=90°, ∠BCF=30°,得∠OCB=60°,再证ΔOCB为等边三角形,得∠COB=60°,可得∠CFO=30°,所以FO=2OC=2OB,FB=OB= OC =2,在直角三角形OCE中,解直角三角形可得CE,再推出CD=2CE.
(1)证明:连接OD
∵CF是⊙O的切线
∴∠OCF=90°
∴∠OCD+∠DCF=90°
∵直径AB⊥弦CD
∴CE=ED,即OF为CD的垂直平分线
∴CF=DF
∴∠CDF=∠DCF
∵OC=OD,
∴∠CDO=∠OCD
∴∠CDO +∠CDB=∠OCD+∠DCF=90°
∴OD⊥DF
∴DF是⊙O的切线
(2)解:连接OD
∵∠OCF=90°, ∠BCF=30°
∴∠OCB=60°
∵OC=OB
∴ΔOCB为等边三角形,
∴∠COB=60°
∴∠CFO=30°
∴FO=2OC=2OB
∴FB=OB= OC =2
在直角三角形OCE中,∠CEO=90°∠COE=60°
![]()
∴CF![]()
∴CD=2 CF![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为__________________元(用含a的代数式表示);
当x≥16时,支付费用为_________________元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
物品重量(千克)
支付费用(元)
18
39
25
53
试根据以上提供的信息确定a,b的值.
(3)根据这个规定,若丙要托运一件超过16千克的物品,但支付的费用不想超过70元,那么丙托运的物品最多是多少千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图
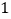 可以得到
可以得到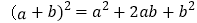 ,基于此,请解答下列问题:
,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,
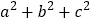 = .
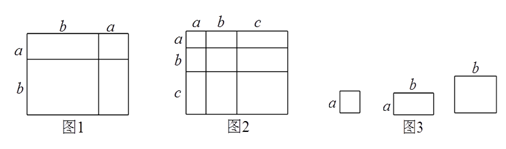
= .(3) 小明同学用图 中x 张边长为a 的正方形, y张边长为b 的正方形,z 张宽、长分别为 a、b 的长方形纸片拼出一个面积为 (2a+b)(a+2b)长方形,则x+y+z=
【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为
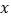 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .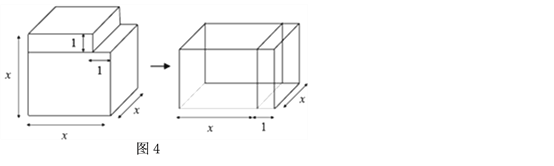
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 和
和 中,
中, ,还需再添加两个条件才能使
,还需再添加两个条件才能使 ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )
A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
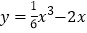 的图象与性质.小彤根据学习函数的经验,对函数
的图象与性质.小彤根据学习函数的经验,对函数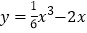 的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:x
-4
-3.5
-3
-2
-1
0
1
2
3
3.5
4
y
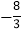
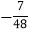


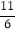
0
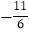
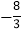
m
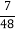

(1)求m的值为 ;
(2)如图,在平面直角坐标系x0y 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程
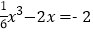 实数根的个数为 ;
实数根的个数为 ; (4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线
 ,根据图象写出方程
,根据图象写出方程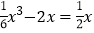 的一个正数根约为 (精确到0.1).
的一个正数根约为 (精确到0.1).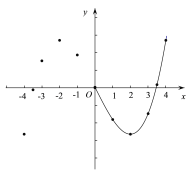
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足
 =0,点C(m,n)在第一象限,已知
=0,点C(m,n)在第一象限,已知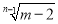 是2的立方根.
是2的立方根.
(1)直接写出A,B,C三点的坐标;
(2)求出△ABC的面积;
(3)如图2,延长BC交y轴于D点,求点D的坐标.
相关试题

