【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足![]() =0,点C(m,n)在第一象限,已知
=0,点C(m,n)在第一象限,已知![]() 是2的立方根.
是2的立方根.

(1)直接写出A,B,C三点的坐标;
(2)求出△ABC的面积;
(3)如图2,延长BC交y轴于D点,求点D的坐标.
参考答案:
【答案】(1)点A的坐标为(0,2),点B的坐标为(8,0),点C的坐标为(4,4);(2)△ABC的面积=12;(3)点D的坐标为(0,8).
【解析】
(1)根据非负数的性质列出方程组分别求出a、b,根据立方根的概念求出m、n,得到A,B,C三点的坐标;
(2)作CE⊥y轴于点E,根据梯形的面积公式、三角形的面积公式计算;
(3)利用待定系数法求出直线BC的解析式,根据坐标轴上点的坐标特征计算,得到答案.
(1)由题意得,![]() ,
,
解得,![]() ,
,
∵![]() 是2的立方根,
是2的立方根,
∴n-1=3,m-2=2,
解得,m=4,n=4,
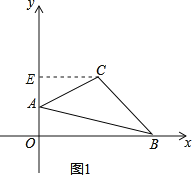
∴点A的坐标为(0,2),点B的坐标为(8,0),点C的坐标为(4,4);
(2)作CE⊥y轴于点E,
则△ABC的面积=梯形EOBC的面积-△AEC的面积-△AOB的面积
=![]() ×(4+8)×4-
×(4+8)×4-![]() ×4×2-
×4×2-![]() ×2×8
×2×8
=12;
(3)设直线BC的解析式为:y=kx+b,
则![]() ,
,
解得,![]() ,
,
∴直线BC的解析式为:y=-x+8,
当y=0时,-x+8=0,
解得,x=8,
∴点D的坐标为(0,8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
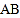 是⊙
是⊙ 的直径,弦
的直径,弦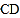
 于点
于点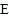 ,过点
,过点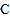 的切线交
的切线交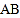 的延长线于点
的延长线于点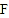 ,连接DF.
,连接DF.(1)求证:DF是⊙
 的切线;
的切线; (2)连接
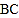 ,若
,若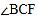 =30°,
=30°,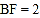 ,求
,求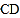 的长.
的长.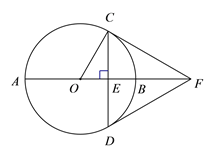
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 和
和 中,
中, ,还需再添加两个条件才能使
,还需再添加两个条件才能使 ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )
A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
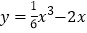 的图象与性质.小彤根据学习函数的经验,对函数
的图象与性质.小彤根据学习函数的经验,对函数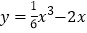 的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:x
-4
-3.5
-3
-2
-1
0
1
2
3
3.5
4
y
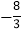
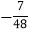


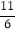
0
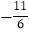
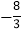
m
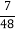

(1)求m的值为 ;
(2)如图,在平面直角坐标系x0y 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程
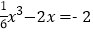 实数根的个数为 ;
实数根的个数为 ; (4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线
 ,根据图象写出方程
,根据图象写出方程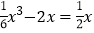 的一个正数根约为 (精确到0.1).
的一个正数根约为 (精确到0.1).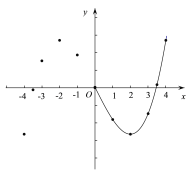
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个.
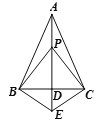
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
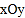 中,抛物线
中,抛物线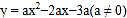 ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在
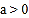 的条件下,当
的条件下,当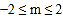 时,n的取值范围是
时,n的取值范围是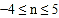 ,求抛物线的表达式;
,求抛物线的表达式;②若D点坐标(4,0),当
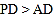 时,求a的取值范围.
时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
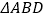 与
与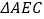 都是等边三角形,
都是等边三角形,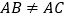 ,下列结论中,正确的个数是( )①
,下列结论中,正确的个数是( )①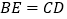 ;②
;②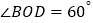 ;③
;③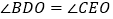 ;④若
;④若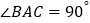 ,且
,且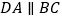 ,则
,则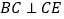 .
.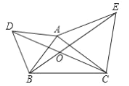
A.1B.2C.3D.4
相关试题

