【题目】【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
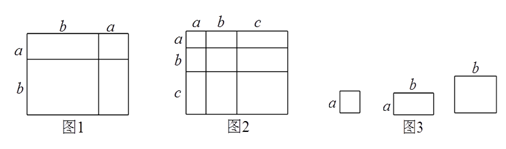
例如图![]() 可以得到
可以得到![]() ,基于此,请解答下列问题:
,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,![]() = .
= .
(3) 小明同学用图 中x 张边长为a 的正方形, y张边长为b 的正方形,z 张宽、长分别为 a、b 的长方形纸片拼出一个面积为 (2a+b)(a+2b)长方形,则x+y+z=
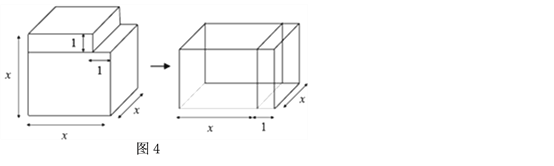
【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为![]() 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
参考答案:
【答案】(1)![]() ; (2) 30; (3) 9 ;
; (2) 30; (3) 9 ;
(4)![]() .
.
【解析】分析:(1)根据图2,利用直接求与间接法分别表示出正方形面积,即可确定出所求等式;
(2)根据(1)中结果,求出所求式子的值即可;
(3)根据已知等式,做出相应图形,即可得到结论;
(4)分别表示出两个图形的体积,由两个图形的体积相等,即可得出结论.
详解:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵a+b+c=10,ab+bc+ac=35,∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=100﹣70=30;
(3)根据题意得:(2a+b)(a+2b)=![]() ,∴x=2,y=5,z=2,∴x+y+z=9;
,∴x=2,y=5,z=2,∴x+y+z=9;
(4)第一个图形的体积=![]() ,第二个图形的体积为:
,第二个图形的体积为:![]() .∵两个图形的体积相等,∴
.∵两个图形的体积相等,∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个含有字母a的同底数幂相乘的运算式子__________,运算结果为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1,在方格纸内将
 经过一次平移后得到
经过一次平移后得到 ,图中标出了点B的对应点
,图中标出了点B的对应点 .根据下列条件,利用网格点和直尺画图:
.根据下列条件,利用网格点和直尺画图:(1)补全
 ;
;(2)作出中线
 ;
;(3)画出
 边上的高线
边上的高线 ;
;(4)在平移过程中,线段
 扫过的面积为 .
扫过的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD平分∠BAC,∠EAD=∠EDA.
(
 )∠EAC与∠B相等吗?为什么?
)∠EAC与∠B相等吗?为什么?(
 )若
)若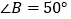 ,
,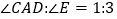 ,则
,则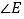 = .
= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形
 中,∠A=∠C=90°.
中,∠A=∠C=90°.(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.

(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.

(3)如图3,若BE、DE分别五等分∠ABC、∠ADC的邻补角(即∠CDE=
 ,∠CBE=
,∠CBE= ),则∠E= .
),则∠E= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF;
(2)若连接AD、CF,则这两条线段之间的关系是________________;
(3)在图中找出所有满足S△ABC=S△QBC的格点Q (异于点A),并用Q1、Q2…表示.

相关试题

