【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
参考答案:
【答案】(1)见解析(2)△ECD可以是等腰三角形,∠AED=105°
【解析】试题分析:(1)、由DE∥BC得到∠BCD=∠CDE=30°,再由∠ACB=120°,得到∠ACD=120°﹣30°=90°,则△ACD是直角三角形;(2)、分类讨论:当∠CDE=∠ECD时,EC=DE;当∠ECD=∠CED时,CD=DE;当∠CED=∠CDE时,EC=CD;然后利用等腰三角形的性质和三角形的内角和定理进行计算.
试题解析:(1)、∵△ABC中,AC=BC, ∴∠A=∠B=![]() =
=![]() =30°,
=30°,
∵DE∥BC, ∴∠ADE=∠B=30°, 又∵∠CDE=30°, ∴∠ADC=∠ADE+∠CDE=30°+30°=60°,
∴∠ACD=180°﹣∠A﹣∠ADC=180°﹣30°﹣60°=90°, ∴△ACD是直角三角形;
(2)、△ECD可以是等腰三角形.理由如下:
①当∠CDE=∠ECD时,EC=DE, ∴∠ECD=∠CDE=30°, ∵∠AED=∠ECD+∠CDE, ∴∠AED=60°,
②当∠ECD=∠CED时,CD=DE, ∵∠ECD+∠CED+∠CDE=180°,
∴∠CED=![]() =
=![]() =75°, ∴∠AED=180°﹣∠CED=105°,
=75°, ∴∠AED=180°﹣∠CED=105°,
③当∠CED=∠CDE时,EC=CD, ∠ACD=180°﹣∠CED﹣∠CDE=180°﹣30°﹣30°=120°,
∵∠ACB=120°, ∴此时,点D与点B重合,不合题意.
综上,△ECD可以是等腰三角形,此时∠AED的度数为60°或105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】144的算术平方根是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点E为BC边上一动点(不与点B、C重合),过点E作射线EF交AC于点F,使∠AEF=∠B.

(1)判断∠BAE与∠CEF的大小关系,并说明理由;
(2)请你探索:当△AEF为直角三角形时,求∠AEF与∠BAE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
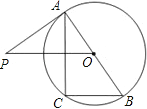
(1)求证:△ABC∽△POA;
(2)若OB=2,OP=
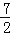 ,求BC的长.
,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发, 到收工时,行走记录为(单位:千米):
+8、-9、+4、+7、-2、-10、+18、-3、+7、+5
回答下列问题:
(1)收工时检修组在A地的哪边?距A地多少千米?
(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果汽车向南行驶30米记作+30米,那么-50米表示( )
A. 向东行驶50米 B. 向西行驶50米 C. 向南行驶50米 D. 向北行驶50米
相关试题

