【题目】有这样一个问题:探究函数![]() 的图象与性质.小彤根据学习函数的经验,对函数
的图象与性质.小彤根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
x | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | ||
y |
|
|
|
|
| 0 |
|
| m |
|
|
(1)求m的值为 ;
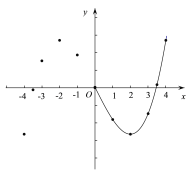
(2)如图,在平面直角坐标系x0y 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程![]() 实数根的个数为 ;
实数根的个数为 ;
(4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线![]() ,根据图象写出方程
,根据图象写出方程![]() 的一个正数根约为 (精确到0.1).
的一个正数根约为 (精确到0.1).
参考答案:
【答案】(1) ![]() ;(2)见解析;(3)3个;(4)见解析;(5)3.87.
;(2)见解析;(3)3个;(4)见解析;(5)3.87.
【解析】(1)由表格可得:x=3,代入![]() ,即可求出y的值.(2)由表格中的x、y的值,描点、连线,进而画出图象;(3)根据函数
,即可求出y的值.(2)由表格中的x、y的值,描点、连线,进而画出图象;(3)根据函数![]() 和直线y=-2的交点的个数即可得出结论;(4)根据函数图象即可得出结论;(5)由
和直线y=-2的交点的个数即可得出结论;(4)根据函数图象即可得出结论;(5)由![]() 与
与![]() 图象交点得出结论.
图象交点得出结论.
(1)![]()
(2)如图所示
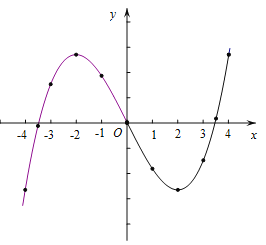
(3)3个
(4)图象关于原点中心对称,x>2时,y随x的增大而增大等(答案不唯一).
(5)如图所示:
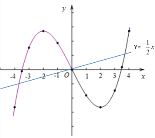
由图象可得一个正数根约为:3.87
-
科目: 来源: 题型:
查看答案和解析>>【题目】【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图
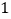 可以得到
可以得到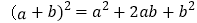 ,基于此,请解答下列问题:
,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,
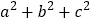 = .
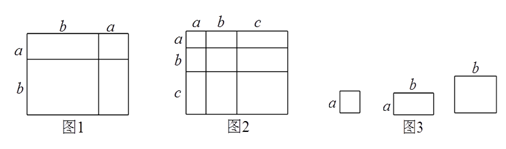
= .(3) 小明同学用图 中x 张边长为a 的正方形, y张边长为b 的正方形,z 张宽、长分别为 a、b 的长方形纸片拼出一个面积为 (2a+b)(a+2b)长方形,则x+y+z=
【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为
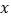 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .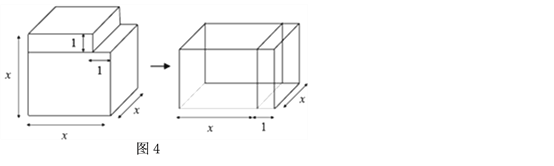
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
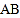 是⊙
是⊙ 的直径,弦
的直径,弦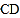
 于点
于点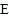 ,过点
,过点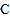 的切线交
的切线交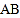 的延长线于点
的延长线于点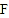 ,连接DF.
,连接DF.(1)求证:DF是⊙
 的切线;
的切线; (2)连接
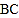 ,若
,若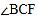 =30°,
=30°,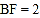 ,求
,求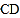 的长.
的长.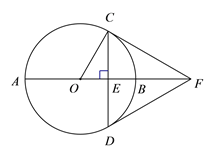
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 和
和 中,
中, ,还需再添加两个条件才能使
,还需再添加两个条件才能使 ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )
A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足
 =0,点C(m,n)在第一象限,已知
=0,点C(m,n)在第一象限,已知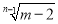 是2的立方根.
是2的立方根.
(1)直接写出A,B,C三点的坐标;
(2)求出△ABC的面积;
(3)如图2,延长BC交y轴于D点,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个.
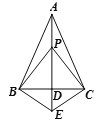
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
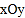 中,抛物线
中,抛物线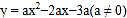 ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在
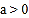 的条件下,当
的条件下,当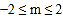 时,n的取值范围是
时,n的取值范围是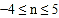 ,求抛物线的表达式;
,求抛物线的表达式;②若D点坐标(4,0),当
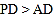 时,求a的取值范围.
时,求a的取值范围.
相关试题

