【题目】如图,在平面直角坐标系中,第一次将三角形OAB变换成三角形OA1B1,第二次将三角形OA1B1变换成三角形OA2B2,第三次将三角形OA2B2变换成三角形OA3B3.
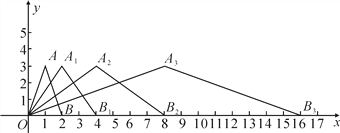
(1)观察每次变换前后的三角形的变化规律,若将三角形OA3B3变换成三角形OA4B4,则A4的坐标是______________,B4的坐标是___________________.
(2)若按第(1)题找到的规律将三角形OAB进行n次变换得到三角形OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是____________,Bn的坐标是_________________.
参考答案:
【答案】(1) (16,3);(32,0)(2)(2n,3);(2n+1,0)
【解析】试题分析:(1)根据题意得出A,B点横纵坐标变化规律,进而得出答案;
(2)结合(1)中发现规律得出一般公式即可.
试题解析:(1)根据题意可知A1的横坐标为2,A2的横坐标为2×2,A3的横坐标为2×2×2,A4的横坐标为2×2×2×2,而点的纵坐标不变,则A4的坐标为(16,3);B1的横坐标为2×2,B2的横坐标为2×2×2,B3的横坐标为2×2×2×2,B4的横坐标为2×2×2×2×2,横坐标不变,故B4的坐标为(32,0).
(2)由(1)可知An的横坐标为2n,Bn的横坐标为2An=2×2n=2n+1,所以An的坐标为(2n,3),Bn的坐标为(2n+1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分)
14
15
16
17
18
19
20
人数(人)
1
3
2
2
1
2
2
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD各顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).
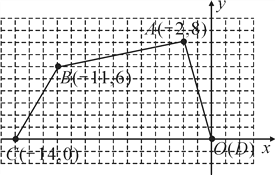
(1)确定这个四边形的面积,你是怎样做的?
(2)如果把四边形ABCD各顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
-
科目: 来源: 题型:
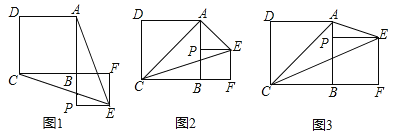
查看答案和解析>>【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B,C,D处的其他甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
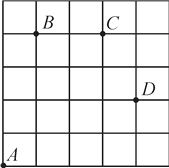
(1)图中B→C(____,____),C→____(+1,____);
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中另有两个格点M,N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记作什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足
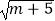 +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处. 
(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点.
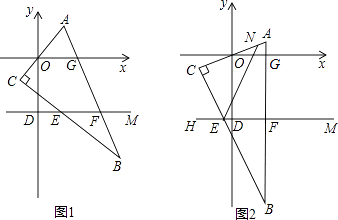
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系: .
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.
相关试题

