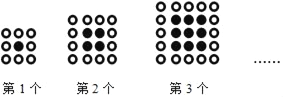
【题目】如图所示,用同样大小的黑、白两种颜色的棋子摆成正方形图案,则下列说法中:①第n个正方形包含(4n+4)枚白色棋子;②第n个正方形包含n2枚黑色棋子;③第n个正方形包含(n+2)2﹣n2枚白色棋子;④第n个正方形一共包含(n+1)2枚棋子,正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
此题可以正方形的周长计算公式为基础,分析图形规律,得出结论,然后代入数值求解即可.
解:第1个正方形图案有棋子共32=9枚,其中黑色棋子有12=1枚,白色棋子有(32﹣12)枚;
第2个正方形图案有棋子共42=16枚,其中黑色棋子有22=4枚,白色棋子有(42﹣22)枚;
…
第n个正方形图案有棋子共(n+2)2枚,其中黑色棋子有n2枚,白色棋子有(n+2)2﹣n2=4(n+1)=4n+4枚;
故①②③正确,④错误
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A,B两点,AB=18,原点O是线段AB上的一点,OA=2OB.
(1)求出A,B两点所表示的数;
(2)若点C是线段AO上一点,且满足 AC=CO+CB,求C点所表示的数;
(3)若点E以3个单位长度/秒的速度从点A沿数轴向点B方向匀速运动,同时点F以1个单位长度/秒的速度从点B沿数轴向右匀速运动,并设运动时间为t秒,问t为多少时,E、F两点重合.并求出此时数轴上所表示的数.
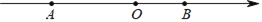
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5.6+(-0.9)+4.4+(-8.1)+(-0.1)
(2)
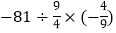
(3)
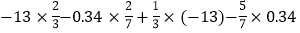
(4)
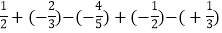
(5)
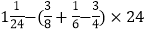
(6)
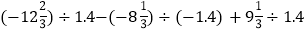
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )

A.5
B.10
C.10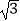
D.15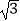
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A. 2个 B. 3个 C. 4个 D. 无数个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)7﹣(﹣3)+(﹣5)
(2)﹣2.5÷

(3)﹣(﹣2)2﹣[(﹣6)2﹣4]
(4)

(5)3ab﹣4ab﹣(﹣2ab)
相关试题

