【题目】已知抛物线![]() 与
与![]() 轴只有一个交点,且与
轴只有一个交点,且与![]() 轴交于
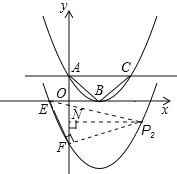
轴交于![]() 点,如图,设它的顶点为B.
点,如图,设它的顶点为B.

(1)求![]() 的值;
的值;
(2)过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线![]() ,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线
,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线![]() 上求点P,使得△
上求点P,使得△![]() 是以EF为直角边的直角三角形?
是以EF为直角边的直角三角形?
参考答案:
【答案】(1)m = 2;(2)证明见解析;(3)满足条件的P点的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
【解析】试题分析:(1)根据抛物线与x轴只有一个交点可知△的值为0,由此得到一个关于m的一元一次方程,解此方程可得m的值;
(2)根据抛物线的解析式求出顶点坐标,根据A点在y轴上求出A点坐标,再求C点坐标,根据三个点的坐标得出△ABC为等腰直角三角形;
(3)根据抛物线解析式求出E、F的坐标,然后分别讨论以E为直角顶点和以F为直角顶点P的坐标.
试题解析:(1)∵抛物线y=x2-2x+m-1与x轴只有一个交点,
∴△=(-2)2-4×1×(m-1)=0,
解得,m=2;
(2)由(1)知抛物线的解析式为y=x2-2x+1=(x-1)2,易得顶点B(1,0),
当x=0时,y=1,得A(0,1).
由1=x2-2x+1,解得,x=0(舍)或x=2,所以C点坐标为:(2,1).
过C作x轴的垂线,垂足为D,则CD=1,BD=xD-xB=1.

∴在Rt△CDB中,∠CBD=45°,BC=![]() .
.
同理,在Rt△AOB中,AO=OB=1,于是∠ABO=45°,AB=![]() .
.
∴∠ABC=180°-∠CBD-∠ABO=90°,AB=BC,
因此△ABC是等腰直角三角形;
(3)由题知,抛物线C′的解析式为y=x2-2x-3,
当x=0时,y=-3;
当y=0时,x=-1或x=3,
∴E(-1,0),F(0,-3),即OE=1,OF=3.
第一种情况:若以E点为直角顶点,设此时满足条件的点为P1(x1,y1),作P1M⊥x轴于M.

∵∠P1EM+∠OEF=∠EFO+∠OEF=90°,
∴∠P1EM=∠EFO,得Rt△EFO∽Rt△P1EM,
则![]() ,即EM=3P1M.
,即EM=3P1M.
∵EM=x1+1,P1M=y1,
∴x1+1=3y1①
由于P1(x1,y1)在抛物线C′上,
则有3(x12-2x1-3)=x1+1,
整理得,3x12-7x1-10=0,解得,
x1=![]() ,或x2=-1(舍去)
,或x2=-1(舍去)
把x1=![]() 代入①中可解得,
代入①中可解得,
y1=![]() .
.
∴P1(![]() ,
, ![]() ).
).
第二种情况:若以F点为直角顶点,设此时满足条件的点为P2(x2,y2),作P2N⊥y轴于N.
同第一种情况,易知Rt△EFO∽Rt△FP2N,
得![]() ,即P2N=3FN.
,即P2N=3FN.
∵P2N=x2,FN=3+y2,
∴x2=3(3+y2)②
由于P2(x2,y2)在抛物线C′上,
则有x2=3(3+x22-2x2-3),
整理得3x22-7x2=0,解得x2=0(舍)或x2=![]() .
.
把x2=![]() 代入②中可解得,
代入②中可解得,
y2=![]() .
.
∴P2(![]() ,
,![]() ).
).
综上所述,满足条件的P点的坐标为:(![]() ,
, ![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下述材料:
我们在学习二次根式时,熟悉的分母有理化以及应用.其实,有一个类似的方法叫做“分子有理化”:
与分母有理化类似,分母和分子都乘以分子的有理化因式,从而消掉分子中的根式比如:

分子有理化可以用来比较某些二次根式的大小,也可以用来处理一些二次根式的最值问题.例如:
比较
 和
和 的大小.可以先将它们分子有理化如下:
的大小.可以先将它们分子有理化如下:

因为
 ,所以
,所以
再例如:求
 的最大值.做法如下:
的最大值.做法如下:解:由
 可知
可知 ,而
,而
当
 时,分母
时,分母 有最小值2,所以的最大值是2.
有最小值2,所以的最大值是2.解决下述问题:
(1)比较
 和
和 的大小;
的大小;(2)求
 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2 是关于x的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
(1)求x1,x2 的值;
(2)若x1,x2 是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生养成良好的“爱读书,读好书,好读书”的习惯,我市某中学举办了“汉字听写大赛”,准备为获奖同学颁奖.在购买奖品时发现,一个书包和一本词典会花去48元,用124元恰好可以购买3个书包和2本词典.
(1)每个书包和每本词典的价格各是多少元?
(2)学校计划总费用不超过900元,为获胜的40名同学颁发奖品(每人一个书包或一本词典),求最多可以购买多少个书包?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图左右并排的两颗大树的高度分别是AB=8米,CD=12米,两树的水平距离BD=5米,一观测者的眼睛高EF=1.6米,且E、B、D在一条直线上,当观测者的视线FAC恰好经过两棵树的顶端时,四边形ABDC的区域是观测者的盲区,则此时观测者与树AB的距离EB等于( )

A.8米 B.7米 C.6米 D.5米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形
 中,点
中,点 在线段
在线段 上,
上,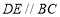 交
交 于点
于点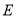 ,点
,点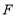 在直线
在直线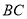 上,作直线
上,作直线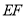 ,过点
,过点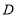 作直线
作直线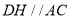 交直线
交直线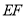 于点
于点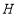 .
.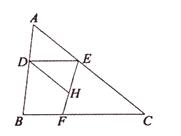
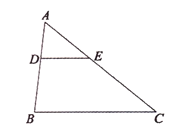
图1 图2 图3
(1)在如图1所示的情况下,求证:
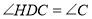 ;
;(2)若三角形
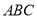 不变,
不变,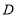 ,
,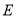 两点的位置也不变,点
两点的位置也不变,点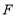 在直线
在直线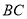 上运动.
上运动.①当点
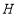 在三角形
在三角形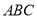 内部时,说明
内部时,说明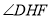 与
与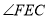 的数量关系:
的数量关系:②当点
 在三角形
在三角形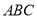 外部时,①中结论是否依然成立?若不成立,
外部时,①中结论是否依然成立?若不成立,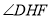 与
与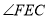 又有怎样的数量关系?请在图2中画图探究,并说明理由.
又有怎样的数量关系?请在图2中画图探究,并说明理由.
相关试题

