Question

【题目】如图，点P是等边三角形ABC内一点，且PA=3，PB=4，PC=5，若将△APB绕着点B逆时针旋转后得到△CQB，则∠APB的度数

Answer 1

【答案】150°
【解析】解：连接PQ，由题意可知△ABP≌△CBQ 则QB=PB=4，PA=QC=3，∠ABP=∠CBQ，
∵△ABC是等边三角形，
∴∠ABC=∠ABP+∠PBC=60°，
∴∠PBQ=∠CBQ+∠PBC=60°，
∴△BPQ为等边三角形，
∴PQ=PB=BQ=4，
又∵PQ=4，PC=5，QC=3，
∴PQ2+QC2=PC2 ，
∴∠PQC=90°，
∵△BPQ为等边三角形，
∴∠BQP=60°，
∴∠BQC=∠BQP+∠PQC=150°
∴∠APB=∠BQC=150°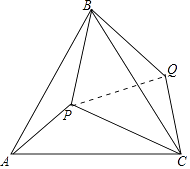

首先证明△BPQ为等边三角形，得∠BQP=60°，由△ABP≌CBQ可得QC=PA，在△PQC中，已知三边，用勾股定理逆定理证出得出∠PQC=90°，可求∠BQC的度数，由此即可解决问题．