【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形,则称该抛物线为“等边抛物线”.
(1)判断抛物线C1:y=![]() x2﹣2
x2﹣2![]() x是否为“等边抛物线”?如果是,求出它的对称轴和顶点坐标;如果不是,说明理由.
x是否为“等边抛物线”?如果是,求出它的对称轴和顶点坐标;如果不是,说明理由.
(2)若抛物线C2:y=ax2+2x+c为“等边抛物线”,求ac的值;
(3)对于“等边抛物线”C3:y=x2+bx+c,当1<x<m时,二次函数C3的图象落在一次函数y=x图象的下方,求m的最大值.
参考答案:
【答案】(1)抛物线y=![]() x2﹣2
x2﹣2![]() x是“等边抛物线”;对称轴x=2,顶点坐标为(2,﹣2
x是“等边抛物线”;对称轴x=2,顶点坐标为(2,﹣2![]() );(2)ac=﹣2;(3)m的最大值为6.
);(2)ac=﹣2;(3)m的最大值为6.
【解析】
(1)根据“等边抛物线”的定义得到抛物线C1:y=![]() x2﹣2
x2﹣2![]() x是“等边抛物线”;然后根据抛物线的性质求得它的对称轴和顶点坐标;
x是“等边抛物线”;然后根据抛物线的性质求得它的对称轴和顶点坐标;
(2)设等边抛物线与x轴的两个交点分别为A(x1,0),B(x2,0),知AB=|x1﹣x2|=|![]() ﹣
﹣![]() |=|
|=|![]() |,结合顶点坐标(﹣
|,结合顶点坐标(﹣![]() ,
,![]() )知
)知 =
=![]() ,据此求解可得;
,据此求解可得;
(3)依照(2)的方法推出b2﹣4ac=12知c=![]() ,结合等边抛物线过(1,1)求得b=﹣6或b=2,依据对称轴位置得b=﹣6,联立
,结合等边抛物线过(1,1)求得b=﹣6或b=2,依据对称轴位置得b=﹣6,联立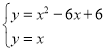 ,求得x=1或x=6,从而得出答案.
,求得x=1或x=6,从而得出答案.
(1)抛物线y=![]() x2﹣2
x2﹣2![]() x是“等边抛物线”.对称轴x=2,顶点坐标为(2,﹣2
x是“等边抛物线”.对称轴x=2,顶点坐标为(2,﹣2![]() ).理由如下:
).理由如下:
由y=![]() x2﹣2
x2﹣2![]() x=
x=![]() x(
x(![]() x﹣2)知,该抛物线与x轴的交点是(0,0),(4,0).
x﹣2)知,该抛物线与x轴的交点是(0,0),(4,0).
又因为y=![]() x2﹣2
x2﹣2![]() x=
x=![]() (x﹣2)2﹣2
(x﹣2)2﹣2![]() ,
,
所以其顶点坐标是(2,﹣2![]() ).
).
∴抛物线与x轴的两个交点及其顶点构成等边三角形的边长为4,
∴抛物线y=![]() x2﹣2
x2﹣2![]() x是“等边抛物线”.
x是“等边抛物线”.
对称轴x=2,顶点坐标为(2,﹣2![]() );
);
(2)设等边抛物线与x轴的两个交点分别为A(x1,0),B(x2,0),
令y=ax2+bx+c=0,
∴x=![]() ,
,
∴AB=|x1﹣x2|=|![]() ﹣
﹣![]() |=|
|=|![]() |=|
|=|![]() |=|
|=|![]() |.
|.
又∵抛物线的顶点坐标为(﹣![]() ,
,![]() ),
),
∴ =
=![]() .
.
∵4﹣4ac≠0,
∴|![]() |=
|=![]() ,
,
∴ac/span>=﹣2;
(3)设等边抛物线与x轴的两个交点分别为A(x1,0),B(x2,0),
令y=ax2+bx+c=0,
∴x=![]() ,
,
∴AB=|x1﹣x2|=|![]() ﹣
﹣![]() |=
|=![]()
又∵抛物线的顶点坐标为![]() ,
,
∴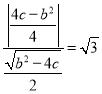 .
.
∵![]() ,
,
∴![]() ,
,
得b2﹣4c=12,
∴c=![]() ,
,
∴C3:y=x2+bx+![]() ,
,
∵1<x<m时,总存在实数b,使二次函数C3的图象在一次函数y=x图象的下方,即抛物线与直线有一个交点为(1,1),
∴该等边抛物线过(1,1),
∴1+b+![]() =1,
=1,
解得b=﹣6或b=2,
又对称轴x=﹣![]() =﹣
=﹣![]() >1,
>1,
∴b<﹣2,
∴b=﹣6,
∴y=x2﹣6x+6,
联立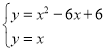 ,
,
解得x=1或x=6,
∴m的最大值为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数
频率
体育
40
0.4
科技
25
a
艺术
b
0.15
其它
20
0.2
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣4,1),B(﹣2,3),C(﹣1,2).
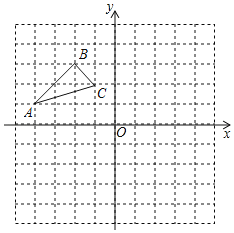
(1)画出△ABC关于原点O成中心对称的△A′B′C′,点A′,B′,C′分别是点A,B,C的对应点.
(2)求过点B′的反比例函数解析式.
(3)判断A′B′的中点P是否在(2)的函数图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=2mx2+5mx﹣12m(m为参数,且m<0)的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0).
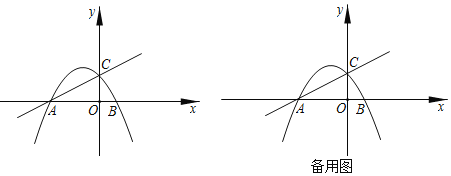
(1)求直线AC的解析式(用含m的式子表示).
(2)若m=﹣
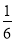 ,连接BC,判断∠CAB和∠CBA的数量关系,并说明理由.
,连接BC,判断∠CAB和∠CBA的数量关系,并说明理由.(3)在(2)的条件下,设点M为AC上方的抛物线上一动点(与点A,C不重合),以M为圆心的圆与直线AC相切,求⊙M面积的取值范围.
-
科目: 来源: 题型:
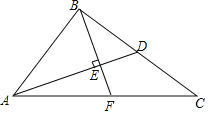
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=4,BC=6,则线段EF的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加学校组织的智力竞答活动,竞赛中有两道单选题完全不会.这两道单选题各有A.B.C三个选项,第一道单选答案是B.第二道单选答案是C.最终两道题小明随机各写了一个答案
(1)小明答对第一道题的概率是 .
(2)请用树状图或者列表求出小明两道题都答对的概率.
相关试题

