【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣4,1),B(﹣2,3),C(﹣1,2).
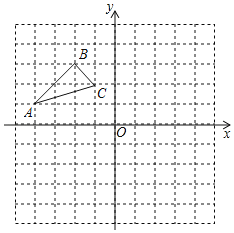
(1)画出△ABC关于原点O成中心对称的△A′B′C′,点A′,B′,C′分别是点A,B,C的对应点.
(2)求过点B′的反比例函数解析式.
(3)判断A′B′的中点P是否在(2)的函数图象上.
参考答案:
【答案】(1)如图,见解析;(2)y=﹣![]() ;(3)点P在(2)的函数图象上.
;(3)点P在(2)的函数图象上.
【解析】
(1)根据关于原点成中心对称的点的坐标特征,即横纵坐标均为相反数,找到对应点,然后依次连线即可.
(2)根据待定系数法,设出反比例函数解析式,然后将B′的坐标代入计算即可.
(3)确定A′B′的中点P的坐标,然后将P点的坐标代入函数解析式,即可解决问题.
(1)∵A(﹣4,1),B(﹣2,3),C(﹣1,2).
关于原点对称的点的坐标横纵坐标均为相反数
∴A′(4,-1),B′(2,-3),C′(1,-2)
在坐标系中找到A′、B′、C′,依次连线即可.
如图:
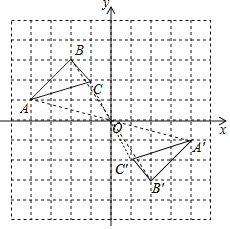
(2)设过点B′的反比例函数解析式为y=![]() ,
,
∵B′(2,﹣3),
∴﹣3=![]() ,
,
∴k=﹣6,
∴反比例函数解析式为y=﹣![]() ;
;
(3)∵A′(4,﹣1),B′(2,﹣3)
∴A′B′的中点P坐标为(3,﹣2),
∵3×(﹣2)=﹣6,
∴点P在(2)的函数图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
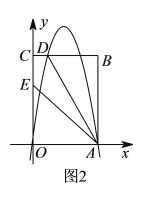
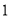 ,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交BC于点D.tan∠OAD=2,抛物线
,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交BC于点D.tan∠OAD=2,抛物线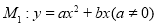 过A,D两点.
过A,D两点.(
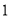 )求点D的坐标和抛物线M1的表达式.
)求点D的坐标和抛物线M1的表达式.(
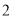 )点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有满足条件的点P的坐标.
)点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有满足条件的点P的坐标.(
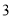 )如图
)如图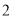 ,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.
,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.①设点D平移后的对应点为点D',当点D'恰好落在直线AE上时,求m的值.
②当
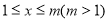 时,若抛物线M2与直线AE有两个交点,求m的取值范围.
时,若抛物线M2与直线AE有两个交点,求m的取值范围.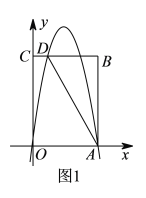
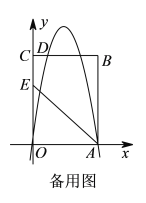
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=2
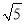 ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.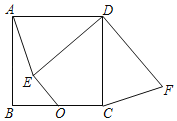
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数
频率
体育
40
0.4
科技
25
a
艺术
b
0.15
其它
20
0.2
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形,则称该抛物线为“等边抛物线”.
(1)判断抛物线C1:y=
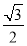 x2﹣2
x2﹣2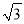 x是否为“等边抛物线”?如果是,求出它的对称轴和顶点坐标;如果不是,说明理由.
x是否为“等边抛物线”?如果是,求出它的对称轴和顶点坐标;如果不是,说明理由.(2)若抛物线C2:y=ax2+2x+c为“等边抛物线”,求ac的值;
(3)对于“等边抛物线”C3:y=x2+bx+c,当1<x<m时,二次函数C3的图象落在一次函数y=x图象的下方,求m的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=2mx2+5mx﹣12m(m为参数,且m<0)的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0).
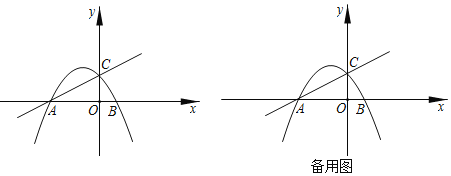
(1)求直线AC的解析式(用含m的式子表示).
(2)若m=﹣
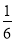 ,连接BC,判断∠CAB和∠CBA的数量关系,并说明理由.
,连接BC,判断∠CAB和∠CBA的数量关系,并说明理由.(3)在(2)的条件下,设点M为AC上方的抛物线上一动点(与点A,C不重合),以M为圆心的圆与直线AC相切,求⊙M面积的取值范围.
相关试题

