【题目】已知,抛物线y=ax+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线![]() 对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
由A(-3,0)和B(2,0),得: ![]()
即 ![]() = ax+bx+4
= ax+bx+4
∴ ![]()
∴ ![]()
∴ ![]() .
.
(2)
易得C(0,4),则BC= ![]() .
.
由 ![]() 可对称轴为x=
可对称轴为x= 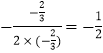 ,
,
则可设点G的坐标为 ![]() ,
,
∵点D是BC的中点
∴点D的坐标为 ![]() ,
, ![]()
由旋转可得,DG=DB
∴ ![]() ……………
……………
∴ ![]() ………
………
∴点G的坐标为 ![]() 或
或 ![]()
(3)
①当BE为对角线时,因为菱形的对角线互相垂直平分,所以此时D即为对称轴与AC的交点或对称轴对BC的交点,F为点D关于x轴的对称点,
设 ![]() ,
,
∵C ![]() ,A
,A ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴当 ![]() 时,
时, ![]() ,
,
∴D ![]() ,
,
∴F ![]() ;
;
易得 ![]()
∴当 ![]() 时,y=5,
时,y=5,
∴D ![]() ,
,
∴F ![]() ;
;
②当BE为菱形的边时,有DF∥BE
I)当点D在直线BC上时
![]()
设D ![]() ,则点F
,则点F ![]()
∵四边形BDFE是菱形
∴FD=DB
根据勾股定理得, ![]()
整理得: ![]() =0,
=0,
解得: ![]() ,
, ![]()
∴F ![]() 或
或 ![]()
II)当点D在直线AC上时
设D ![]() ,则点F
,则点F ![]()
∵四边形BFDE是菱形,
∴FD=FB,
根据勾股定理得, ![]()
整理得: ![]() ,
,
解得: ![]() (舍去),
(舍去), ![]()
∴F ![]() ,
,
综上所述,点F的坐标分别为: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
【解析】(1)可将三个点的分别代入抛物线可解出;或都运用两点式简便求解;(2)由旋转可得DG=DB,因为D是BC中点,所以DB= ![]() BC,求DB的长,和D的坐标,因为G在对称轴上的点,则横坐标为
BC,求DB的长,和D的坐标,因为G在对称轴上的点,则横坐标为 ![]() ,由勾股定理构造方程,解出G的纵坐标;(3)分类讨论:BE在x轴上,所以当BE为对角线上时,则FD也为对角线,它们互相平分且垂直,而点F在对称轴上,D也在对称轴上,所以点D与F关于x轴对称,则点D为AC与对称轴的交点,BC与对称轴的交点,求出点D即可;当BE为边时,根据对边平行可得必有DF//BE,则D,F的纵坐标相等,则当点D在BC上时,可设点D的坐标,从而可得点F的坐标由FD=DB,构造方程解得D的坐标,F的坐标;当点D在AC上时,同理.
,由勾股定理构造方程,解出G的纵坐标;(3)分类讨论:BE在x轴上,所以当BE为对角线上时,则FD也为对角线,它们互相平分且垂直,而点F在对称轴上,D也在对称轴上,所以点D与F关于x轴对称,则点D为AC与对称轴的交点,BC与对称轴的交点,求出点D即可;当BE为边时,根据对边平行可得必有DF//BE,则D,F的纵坐标相等,则当点D在BC上时,可设点D的坐标,从而可得点F的坐标由FD=DB,构造方程解得D的坐标,F的坐标;当点D在AC上时,同理.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:

七年级兴趣班报名情况统计表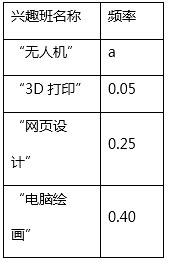
(1)报名参加兴趣班的总人数为人;统计表中的a=;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.

(1)求证:∠ECD=∠EDC;
(2)若tanA= ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数
 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a , b).
的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a , b).
①若 ,请用含n的代数式表示
,请用含n的代数式表示  ;
;
②求证: ;
;
(2)应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数
 的图象交于点C,D两点(点C在点D的左边),已知
的图象交于点C,D两点(点C在点D的左边),已知  ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把
 个边长为1的正方形拼接成一排,求得
个边长为1的正方形拼接成一排,求得  ,
,  ,
,  ,计算
,计算 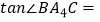 , ……按此规律,写出
, ……按此规律,写出  (用含
(用含  的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形
 )靠墙摆放,高
)靠墙摆放,高  ,宽
,宽  ,小强身高
,小强身高  ,下半身
,下半身 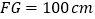 ,洗漱时下半身与地面成
,洗漱时下半身与地面成 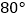 (
(  ),身体前倾成
),身体前倾成  (
(  ),脚与洗漱台距离
),脚与洗漱台距离  (点
(点  ,
,  ,
,  ,
,  在同一直线上).
在同一直线上).
(1)此时小强头部 点与地面
点与地面  相距多少?
相距多少?
(2)小强希望他的头部 恰好在洗漱盆
恰好在洗漱盆  的中点
的中点  的正上方,他应向前或后退多少?
的正上方,他应向前或后退多少?
( ,
,  ,
, 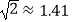 ,结果精确到
,结果精确到  )
)
相关试题

