搜索
【题目】如图是某小区的一个健向器材，已知BC=0.15m，AB=2.70m，∠BOD=70°，求端点A到地面CD的距离（精确到0.1m）.（参考数据：sin70°≈0.94，cos70°≈0.34,tan70°≈2.75）
参考答案：
【答案】解：过点A作AE⊥CD于点E，过点B作BF⊥AE于点F，
∵OD⊥CD，∠BOD=70°，∴AE//OD，∴∠A=∠BOD=70°，
在Rt△AFB中，AB=2.7，∴AF=2.7cos70°=2.7×0.34=0.918,
∴AE=AF+BC=0.918+0.15=1.068≈1.1（m）.
答：端点A到地面CD的距离约是1.1m.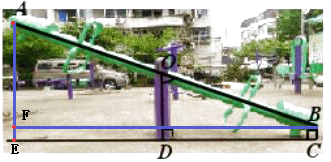
【解析】求求端点A到地面CD的距离，则可过点A作AE⊥CD于点E，在构造直角三角形，可过点B作BF⊥AE于点F，即在Rt△AFB中，AB已知，且∠A=∠BOD=70°，即可求出AF的长，则AE=AF+EF即可求得答案.
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题
（1）探究：如图1 ，直线l与坐标轴的正半轴分别交于A，B两点，与反比例函数
的图象交于C，D两点(点C在点D的左边)，过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F，CE与DF交于点G(a ， b).
①若
，请用含n的代数式表示 
；
②求证：
；
（2）应用：如图2，直线l与坐标轴的正半轴分别交于点A，B两点，与反比例函数 的图象交于点C，D两点(点C在点D的左边)，已知 
，△OBD的面积为1，试用含m的代数式表示k.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，抛物线y=ax+bx+4与x轴交于点A（-3，0）和B（2，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）如图1，若点D为CB的中点，将线段DB绕点D旋转，点B的对应点为点G，当点G恰好落在抛物线的对称轴上时，求点G的坐标；
（3）如图2，若点D为直线BC或直线AC上的一点，E为x轴上一动点，抛物线
对称轴上是否存在点F，使以B，D，F，E为顶点的四边形为菱形？若存在，请求出点F的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把
个边长为1的正方形拼接成一排，求得 
， 
， 
，计算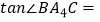 
， ……按此规律，写出 
（用含 的代数式表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是小强洗漱时的侧面示意图，洗漱台（矩形
）靠墙摆放，高 
，宽 
，小强身高 
，下半身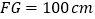 
，洗漱时下半身与地面成 
（ 
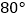），身体前倾成 
（ 
），脚与洗漱台距离 
（点 
， 
， 
， 
在同一直线上）．
（1）此时小强头部
点与地面 
相距多少？
（2）小强希望他的头部 恰好在洗漱盆 
的中点 
的正上方，他应向前或后退多少？
（
， 
， 
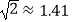，结果精确到 
） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m.
（结果精确到0.1m。参考数据：tan20°≈0.36,tan18°≈0.32）
（1）求∠BCD的度数.
（2）求教学楼的高BD -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧与墙MN平行且距离为0.8米，已知小汽车车门宽AO为1.2米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？请说明理由。（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）
相关试题
