【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)求证:∠ECD=∠EDC;
(2)若tanA= ![]() ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
参考答案:
【答案】
(1)
证明:连结OD,
∵DE是⊙O的切线,∴∠EDC+∠ODA=90°,
又∵OA⊥OB,∴∠ACO+∠A=90°,
∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)
解:∵tanA= ![]() ,∴
,∴ ![]() ,∴OC=2,
,∴OC=2,
设DE=x,∵∠ECD=∠EDC,∴CE=x,∴OE=2+x.
∵∠ODE=90°,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
(3)
解:过点D作AO的垂线,交AO的延长于F,
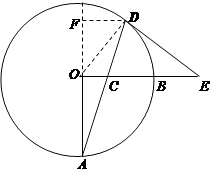
当 ![]() 时,则
时,则 ![]() ,DF=4,
,DF=4,
![]()
当 ![]() 时,
时, ![]() ,DF=4
,DF=4 ![]() ,
,
![]() ,
,
![]()
![]()
![]()
【解析】(1)运用切线的性质以及对顶角相等,角的等量代换可证得;(2)由tanA= ![]() ,可解出OC,由(1)得∠ECD=∠EDC , 等角对等边,则EC=DE,由勾股定理得OD2+DE2=OE2 , 构造方程解出DE的长;(3)分别求出
,可解出OC,由(1)得∠ECD=∠EDC , 等角对等边,则EC=DE,由勾股定理得OD2+DE2=OE2 , 构造方程解出DE的长;(3)分别求出 ![]() 和
和 ![]() 时,弓形ABD的面积,再用前者减去后者即可得到答案.
时,弓形ABD的面积,再用前者减去后者即可得到答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.

(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.

(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70) -
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:

七年级兴趣班报名情况统计表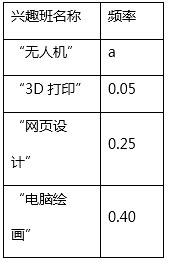
(1)报名参加兴趣班的总人数为人;统计表中的a=;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍? -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数
 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a , b).
的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a , b).
①若 ,请用含n的代数式表示
,请用含n的代数式表示  ;
;
②求证: ;
;
(2)应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数
 的图象交于点C,D两点(点C在点D的左边),已知
的图象交于点C,D两点(点C在点D的左边),已知  ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.

(1)求抛物线的解析式;
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线 对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把
 个边长为1的正方形拼接成一排,求得
个边长为1的正方形拼接成一排,求得  ,
,  ,
,  ,计算
,计算 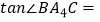 , ……按此规律,写出
, ……按此规律,写出  (用含
(用含  的代数式表示).
的代数式表示).
相关试题

