【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末![]() 位能被
位能被![]() 整除的数,本身必能被
整除的数,本身必能被![]() 整除,反过来,末
整除,反过来,末![]() 位不能被
位不能被![]() 整除的数,本身也不可能被
整除的数,本身也不可能被![]() 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
![]() ,
,![]() 为整数,
为整数,![]() 能被25整除
能被25整除
![]() ,
,![]() 不为整数,
不为整数,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若![]() 这个三位数能被11整除,则
这个三位数能被11整除,则![]() ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
参考答案:
【答案】(1)m=8,68244;(2)这个数为580250或500500或530750或550000.
【解析】
(1)奇数位分别是6和2,偶数为是m,根据题意可知6+2m能被11整除,且m为0至9的数,从而可求出m的值.设该五位数为![]() ,由题意可知a+b=8,且设ba=11n,从而求出a、b的值.
,由题意可知a+b=8,且设ba=11n,从而求出a、b的值.
(2)设这个六位数p为![]() ,根据题意可知:b=2e,所以e只能取0或1或2或3或4,由材料一可知:
,根据题意可知:b=2e,所以e只能取0或1或2或3或4,由材料一可知:![]() 能被125整除,可知
能被125整除,可知![]() =250或500或750,然后分情况求出a、b、c、d、e的值.
=250或500或750,然后分情况求出a、b、c、d、e的值.
解:(1)奇数位分别是6和2,偶数为是m,
∴由材料可知:6+2m能被11整除,
∵0≤m≤9,且m是正整数,
∴m=8,
设该五位数为![]() ,
,
∴奇数位之和为:b+2+6,偶数位之和为:a+8,
∴根据题意可知:8+b8a=ba能被11整除,
∴设ba=11n,n为整数,
∵a+b=8,
∴![]() ,
,
∴解得: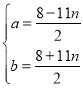 ,
,
∵0≤a≤9,0≤b≤9,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴n=0,
∴a=4,b=4,
∴该数为68244;
(2)设这个六位数p为![]() ,
,
由题意可知:b=2e,
∵0≤b≤9,
∴0≤e≤4.5,
∴e=0或1或2或3或4,
∵![]() 能被125整除,
能被125整除,
∴![]() =125n,n为正整数,
=125n,n为正整数,
∴1≤n≤7,
∵e=0或1或2或3或4,
∴n=2或4或6,
∴![]() =250或500或750或000
=250或500或750或000
∵偶数位之和为:5+b+d=5+2e+d,奇数位之和为:a+c+e,
∴|(5+2e+d)(a+c+e)|=|5+e+dac|能被11整除,
当![]() =250时,
=250时,
∴c=2,d=5,e=0,b=0,
∴|5+e+dac|=|8a|,
设|8a|=11m,m为正整数,
∴a=8±11m,
∵0≤a≤9,
∴![]() ≤m≤
≤m≤![]() 或
或![]() ≤m≤
≤m≤![]() ,
,
∴m=0
∴a=8,
∴该数为580250,
同理:当![]() =500时,该数为500500,
=500时,该数为500500,
当![]() =750时,该数为530750,
=750时,该数为530750,
当![]() =000时,该数为550000
=000时,该数为550000
综上所述,该数为580250或500500或530750或550000.
-
科目: 来源: 题型:
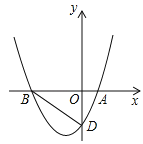
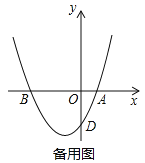
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
 x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.(1)求抛物线的解析式;
(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,四边形PBQD能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;
(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了
 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出
 =___________,
=___________, =_____________;
=_____________;(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
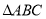 中,
中,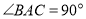 ,
,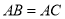 ,点
,点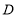 在直线
在直线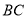 上,
上,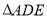 是等腰直角三角形,
是等腰直角三角形,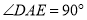 ,
,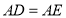 ,连接
,连接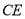 .
.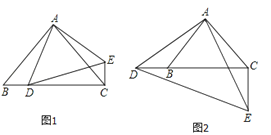
(1)当点
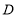 在线段
在线段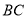 上时,如图1,求证:
上时,如图1,求证: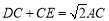 ;
;(2)当点
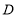 在线段
在线段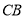 延长线上时,如图2,求证:
延长线上时,如图2,求证: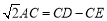
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③.

(1)图②有__________个三角形;图③有________个三角形;
(2)按上面的方法继续下去,第10个图有_________个三角形,第
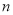 个图形中有_______个三角形.(用含
个图形中有_______个三角形.(用含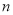 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为﹣6,点B在数轴上A点右侧,且AB=14,动点M从点A出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)写出数轴上点B表示的数 ,点M表示的数 (用含t的式子表示);
(2)动点N从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点M,N同时出发,问点M运动多少秒时追上点N?
(3)若P为AM的中点,F为MB的中点,点M在运动过程中,线段PF的长度是否发生变化?若变化,请说明理由;若不变,请求出线段PF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n以及表中x的值.

相关试题

