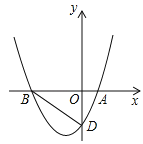
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
(1)求抛物线的解析式;
(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,四边形PBQD能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;
(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.
参考答案:
【答案】(1)y=![]() x2+x﹣4;(2)满足条件的P的坐标为(﹣1,﹣2+
x2+x﹣4;(2)满足条件的P的坐标为(﹣1,﹣2+![]() )或(﹣1.﹣2﹣
)或(﹣1.﹣2﹣![]() );(3)满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+
);(3)满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+![]() ,4).
,4).
【解析】(1)、利用待定系数法求出函数解析式;(2)、分BD为矩形的边和BD为矩形的对角线两种情况分别求出点P的坐标;(3)、设M(m,![]() m2+m﹣4),设直线AM的解析式为y=kx+b,然后求出直线AM的解析式,然后分点M所在的象限,证明出△MNB和△BOC相似,从而分别得出点M的坐标.
m2+m﹣4),设直线AM的解析式为y=kx+b,然后求出直线AM的解析式,然后分点M所在的象限,证明出△MNB和△BOC相似,从而分别得出点M的坐标.
(1)、由题意![]() ,解得
,解得![]() ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x2+x﹣4.
x2+x﹣4.
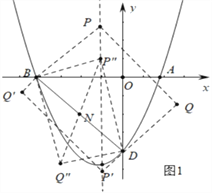
(2)如图1中,当BD为矩形的边时,∵直线BD的解析式为y=﹣x﹣4,
∴直线BP的解析式为y=x=4,直线 DP′的解析式为y=x﹣4,
可得P(﹣1,3),P′(﹣1,﹣5).
当BD为矩形的对角线时,设P(﹣1,m),BD的中点N(﹣2,﹣2),由BN=P″N,
可得12+(m+2)2=(2![]() )2, 解得m=﹣2+
)2, 解得m=﹣2+![]() 或﹣2﹣
或﹣2﹣![]() ,
,
∴P″(﹣1,﹣2+![]() ),或(﹣1.﹣2﹣
),或(﹣1.﹣2﹣![]() ),
),
∴要使四边形PBQD能成为矩形,满足条件的点P坐标为(﹣1,﹣2+![]() )或(﹣1.﹣2﹣
)或(﹣1.﹣2﹣![]() ).
).
综上所述,满足条件的P的坐标为(﹣1,﹣2+![]() )或(﹣1.﹣2﹣
)或(﹣1.﹣2﹣![]() ).
).
(3)设M(m,![]() m2+m﹣4),设直线AM的解析式为y=kx+b,则有
m2+m﹣4),设直线AM的解析式为y=kx+b,则有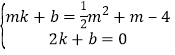 ,
,
解得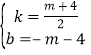 ,∴直线AM的解析式为y=
,∴直线AM的解析式为y=![]() x﹣m﹣4,∴C(0,﹣m﹣4).
x﹣m﹣4,∴C(0,﹣m﹣4).
①点M在第二象限显然不可能,当点M在第三象限时,如图2中,作MN⊥OB于N.
∵∠MBN=∠BCO,∠MNB=∠BOC=90°,∴△MNB∽△BOC,∴![]() ,
,
∴![]() =
=![]() ,∴m=﹣2或0.∴M(﹣2,﹣4)或(0,﹣4).
,∴m=﹣2或0.∴M(﹣2,﹣4)或(0,﹣4).
②当点M在第一象限时,同法可得![]() =
=![]() ,整理得:m2+2m﹣16=0,
,整理得:m2+2m﹣16=0,
∴m=﹣1+![]() 或﹣1﹣
或﹣1﹣![]() (舍弃),∴M(﹣1+
(舍弃),∴M(﹣1+![]() ,4),
,4),
③当点M在第四象限时,不存在,
综上所述,满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+![]() ,4).
,4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
 对应的数为
对应的数为 ,点
,点 对应的数为8,点
对应的数为8,点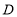 对应的数为
对应的数为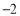 ,
,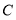 为原点.
为原点.(1)
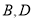 两点的距离是_____;
两点的距离是_____;(2)若点
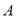 以每秒5个单位长度的速度沿数轴正方向运动,则2秒时
以每秒5个单位长度的速度沿数轴正方向运动,则2秒时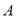 ,
,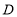 两点的距离是_____;
两点的距离是_____;(3)若点
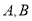 都以每秒4个单位长度的速度沿数轴正方向运动,而点
都以每秒4个单位长度的速度沿数轴正方向运动,而点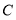 不动,
不动,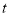 秒时,
秒时,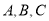 中有一点是三点所在线段的中点,求
中有一点是三点所在线段的中点,求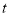 的值.
的值.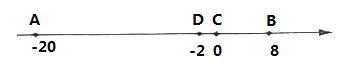
-
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童游乐园门票价格规定如下表:
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1218元.问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?
(3)如果七年级(1)班有10名学生因学校有任务不能参加这次旅游,请你为两个班设计出购买门票的方案,并指出最省钱的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答:(1)若一个多项式与
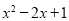 的和是
的和是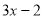 ,求这个多项式.
,求这个多项式.(2)已知
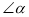 和
和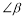 互余,且
互余,且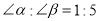 ,求
,求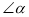 和
和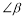 的补角各是多少度?
的补角各是多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了
 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出
 =___________,
=___________, =_____________;
=_____________;(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
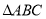 中,
中,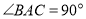 ,
,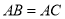 ,点
,点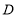 在直线
在直线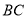 上,
上,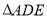 是等腰直角三角形,
是等腰直角三角形,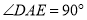 ,
,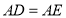 ,连接
,连接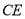 .
.
(1)当点
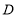 在线段
在线段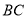 上时,如图1,求证:
上时,如图1,求证: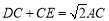 ;
;(2)当点
 在线段
在线段 延长线上时,如图2,求证:
延长线上时,如图2,求证: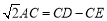
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末
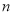 位能被
位能被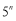 整除的数,本身必能被
整除的数,本身必能被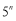 整除,反过来,末
整除,反过来,末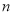 位不能被
位不能被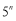 整除的数,本身也不可能被
整除的数,本身也不可能被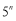 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算: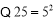 ,
,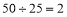 为整数,
为整数,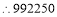 能被25整除
能被25整除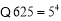 ,
,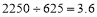 不为整数,
不为整数,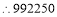 不能被625整除
不能被625整除材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若
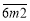 这个三位数能被11整除,则
这个三位数能被11整除,则 ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
相关试题

