【题目】如图,已知数轴上点A表示的数为﹣6,点B在数轴上A点右侧,且AB=14,动点M从点A出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点M表示的数 (用含t的式子表示);
(2)动点N从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点M,N同时出发,问点M运动多少秒时追上点N?
(3)若P为AM的中点,F为MB的中点,点M在运动过程中,线段PF的长度是否发生变化?若变化,请说明理由;若不变,请求出线段PF的长.
参考答案:
【答案】(1)8,5t﹣6;(2)点M运动7秒时追上点N;(3)线段PF的长度不发生变化,PF的长为:7.
【解析】
(1)根据点A表示的数,结合AB与AM的长,即可求解;
(2)设点M运动t秒时追上点N,列出关于t的方程,即可求解;
(3)根据点A,M,B在数轴上表示的数,P为AM的中点,F为MB的中点,进而得出点P,F表示的数,即可求解.
(1)∵AB=14,
∴点B表示的数为:14﹣6=8,
∵MA=5t,
∴点M表示的数为5t﹣6,
故答案为:8,5t﹣6;
(2)设点M运动t秒时追上点N,
∴5t=3t+14,
解得:t=7,
答:点M运动7秒时追上点N;
(3)∵点M表示的数为:5t﹣6,P为AM的中点,F为MB的中点,
∴点P表示的数为:![]() ,点F表示的数为:
,点F表示的数为:![]() ,
,
∴PF=![]() =7,
=7,
∴线段PF的长度不发生变化,PF的长为:7.
-
科目: 来源: 题型:
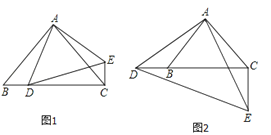
查看答案和解析>>【题目】如图,
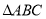 中,
中,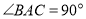 ,
,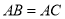 ,点
,点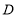 在直线
在直线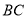 上,
上,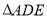 是等腰直角三角形,
是等腰直角三角形,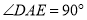 ,
,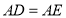 ,连接
,连接 .
.
(1)当点
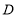 在线段
在线段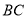 上时,如图1,求证:
上时,如图1,求证: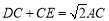 ;
;(2)当点
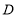 在线段
在线段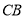 延长线上时,如图2,求证:
延长线上时,如图2,求证: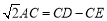
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末
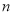 位能被
位能被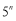 整除的数,本身必能被
整除的数,本身必能被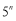 整除,反过来,末
整除,反过来,末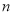 位不能被
位不能被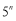 整除的数,本身也不可能被
整除的数,本身也不可能被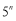 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算: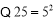 ,
,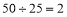 为整数,
为整数,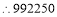 能被25整除
能被25整除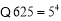 ,
,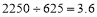 不为整数,
不为整数,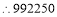 不能被625整除
不能被625整除材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若
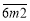 这个三位数能被11整除,则
这个三位数能被11整除,则 ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③.

(1)图②有__________个三角形;图③有________个三角形;
(2)按上面的方法继续下去,第10个图有_________个三角形,第
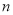 个图形中有_______个三角形.(用含
个图形中有_______个三角形.(用含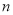 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n以及表中x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从点A看一山坡上的电线杆PQ,观测杆顶端点P的仰角是45°,向前走6 m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度(精确到0.1 m).
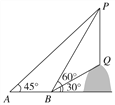
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

相关试题

