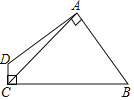
【题目】如图,四边形ABCD中,AB=AD,AC=6,∠DAB=∠DCB=90°,则四边形ABCD的面积为_____.
参考答案:
【答案】18
【解析】
根据已知线段关系,将△ACD绕点A逆时针旋转90°,AD与AB重合,得到△ABE,证明C、B、E三点共线,则△ACE是等腰直角三角形,四边形面积转化为△ACE面积.
∵AD=AD,且∠DAB=90°,
∴将△ACD绕点A逆时针旋转90°,AD与AB重合,得到△ABE.
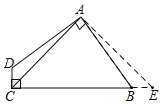
∴∠ABE=∠D,AC=AE.
根据四边形内角和360°,可得∠D+∠ABC=180°
∴∠ABE+∠ABC=180°.
∴C、B、E三点共线.
∴△ACE是等腰直角三角形.
∵四边形ABCD面积=△ACE面积=![]() ×AC2=
×AC2=![]() ×62=18;
×62=18;
故答案为:18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张边长为40 cm的正方形硬纸板,进行适当的裁剪,折成一个长方体盒子(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.

①要使折成的长方体盒子的底面积为484 cm2,那么剪掉的正方形的边长为多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子.若折成的一个长方体盒子的表面积为550 cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是线段
是线段 上的任意一点(端点除外),分别以
上的任意一点(端点除外),分别以 ,
, 为斜边并且在
为斜边并且在 的同一侧作等腰直角
的同一侧作等腰直角 和
和 ,连接
,连接 交
交 于点
于点 ,连接
,连接 交
交 于点
于点 ,给出以下三个结论:①
,给出以下三个结论:① ;②
;② ;③
;③ ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若
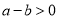 ,则
,则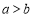 ;若
;若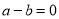 ,则
,则 ;若
;若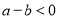 ,则
,则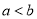 .
.例:已知
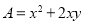 ,
,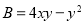 ,其中
,其中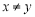 ,求证:
,求证: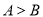 .
.证明:
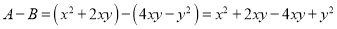
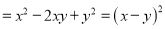 .
.∵
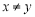 ,∴
,∴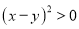 ,∴
,∴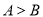 .
.(1)操作感知:比较大小:
①若
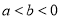 ,则
,则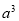 ______
______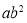 ;
;②
 ______
______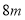 .
.(2)类比探究:已知
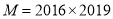 ,
,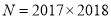 ,试运用上述方法比较
,试运用上述方法比较 、
、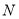 的大小,并说明理由.
的大小,并说明理由.(3)应用拓展:已知
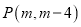 ,
, 为平面直角坐标系中的两点,小明认为,无论
为平面直角坐标系中的两点,小明认为,无论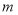 取何值,点
取何值,点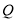 始终在点
始终在点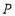 的上方,小明的猜想对吗?为什么?
的上方,小明的猜想对吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
-
科目: 来源: 题型:
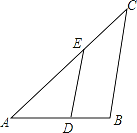
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
相关试题

