【题目】如图,已知四边形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,对角线
,对角线![]() .
.
![]() 求证:四边形
求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,若动点
,若动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒
秒![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
![]() 如图
如图![]() ,若点
,若点![]() 在对角线
在对角线![]() 上,
上,![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 运动至点
运动至点![]() 止.设点
止.设点![]() 运动了
运动了![]() 秒,请你探索:从运动开始,经过多少时间,以点
秒,请你探索:从运动开始,经过多少时间,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?请求出所有可能的结果.
为顶点的三角形是等腰三角形?请求出所有可能的结果.

参考答案:
【答案】(1)详见解析;(2)![]() ;(3)从运动开始,经过
;(3)从运动开始,经过![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,以点
秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.
【解析】
(1)先判定四边形ABCD是平行四边形,再根据∠B=90°,得出四边形ABCD是矩形;
(2)先过Q作QM⊥BC于M点,AP与BQ交于点N,判定△ABP∽△BMQ,得出![]() =
=![]() ,即
,即![]() =
=![]() ,求得t的值即可;
,求得t的值即可;
(3)分为三种情况讨论:当CQ=CP=4cm时,当PQ=CQ=4cm时,当QP=CP时,分别根据等腰三角形的性质,求得BP的长,进而得到t的值.
![]() 证明:∵
证明:∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形;
是矩形;
![]() 如图,过
如图,过![]() 作
作![]() 于
于![]() 点,
点,![]() 与
与![]() 交于点
交于点![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
![]() 分为三种情况:
分为三种情况:
①如图![]() 所示,当
所示,当![]() 时,
时,![]() ,
,

∴![]() 秒;
秒;
②如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∵![]() ,
,![]() ,
,

∴![]() ,
,
∴![]() ,
,
∴![]() 秒;
秒;
③如图![]() 所示,当
所示,当![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
![]() ,
,![]() ,
,
∵![]() ,
,

∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 秒.
秒.
综上所述,从运动开始,经过![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,以点
秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.
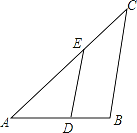
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中C为
 的中点,BC=
的中点,BC= ,O到AB的距离为1,则半径的长( )
,O到AB的距离为1,则半径的长( )
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC中,AM为边BC上的中线,动点D在直线AM上,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
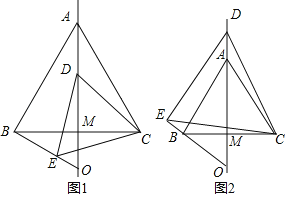
(1)如图1,点D在线段AM上时,填空:
①线段AD与BE的数量关系是 ②∠AOB的度数是 .
(2)如图2,当动点D在线段MA的延长线上时,试判断(1)中的结论是否成立?若成立,请给予证明:若不成立,请写出新的结论,并说明理由.
-
科目: 来源: 题型:
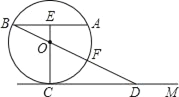
查看答案和解析>>【题目】如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
①求证:EC⊥CD;
②当EO:OC=1:3,CD=4时,求⊙O的半径.
相关试题

