【题目】某餐厅中,一张桌子可以坐6人,如果把多张桌子摆在一起,可以有以下两种摆放方式.
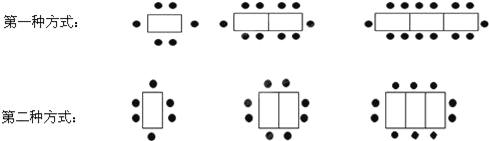
(1)当有5张桌子时,第一种摆放方式能坐 人,第二种摆放方式能坐 人,
(2)当有n张桌子时,第一种摆放方式能坐 人,第二种摆放方式能坐 人,
(3)一天中午餐厅要接待98位顾客共同就餐(即桌子要摆在一起),但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
参考答案:
【答案】(1)22;14;(2)4n+2;2n+4;(3)选用第一种摆放方式.
【解析】试题分析:
(1)、(2):分析两种排列方式的规律可知,第一种排列方式中,每张桌子上下两方共有4个座位,整列桌子的左右两端共有2个座位,由此可知当有n张桌子时,共有(4n+2)个座位;第二种排列方式中,每张桌子的上下两方共有2个座位,整列桌子的左右两端共有4个座位,由此可知当有n张桌子时,共有(2n+4)个座位;
(3)把n=25,代入(2)中所得式子计算比较即可得出结论.
试题解析:
(1)当有5张桌子时,第一种摆放方式能坐4×5+2=22(人);
第二种摆放方式能坐2×5+4=14(人);
(2)第一种中,每张桌子上下两方共有4个座位,整列桌子的左右两端共有2个座位,由此可知当有n张桌子时,能坐(4n+2)个人;
每张桌子的上下两方共有2个座位,整列桌子的左右两端共有4个座位,由此可知当有n张桌子时,能坐(2n+4)个人;
(3)打算用第一种摆放方式来摆放餐桌.
∵当n=25时,第一种方式共有座位:4×25+2=102>98,
当n=25时,第二种方式共有座位:2×25+4=54<98,
∴选用第一种摆放方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与发现
(1)正方形ABCD中有菱形PEFG,当它们的对角线重合,且点P与点B重合时(如图1),通过观察或测量,猜想线段AE与CG的数量关系,并证明你的猜想;
(2)当(1)中的菱形PEFG沿着正方形ABCD的对角线平移到如图2的位置时,猜想线段AE与CG的数量关系,只写出猜想不需证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D、E分别是BC、BA的中点,连接DE,F在DE延长线上,且AF=AE.求证:四边形ACEF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

-
科目: 来源: 题型:
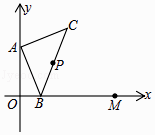
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知凸四边形ABCD中,∠A=∠C=90°.


(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点
 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米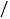 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米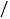 秒,则当△BPD与△CQP全等时,v的值为( )
秒,则当△BPD与△CQP全等时,v的值为( )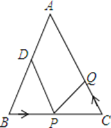
A. 2.5 B. 3 C. 2.25或3 D. 1或5
相关试题

