【题目】已知凸四边形ABCD中,∠A=∠C=90°.


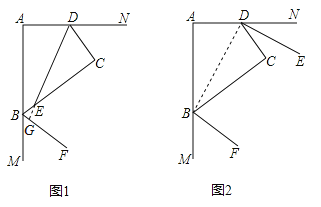
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
参考答案:
【答案】见解析
【解析】试题分析:(1)DE⊥BF,延长DE交BF于G.易证∠ADC=∠CBM.可得∠CDE=∠EBF.即可得∠EGB=∠C=90゜,则可证得DE⊥BF;
(2)DE∥BF,连接BD,易证∠NDC+∠MBC=180゜,则可得∠EDC+∠CBF=90゜,继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜,则可得DE∥BF.
试题解析:解:(1)DE⊥BF.证明如下:
延长DE交BF于点G.∵∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,∴∠ABC+∠ADC=180°.∵∠ABC+∠MBC=180°,∴∠ADC=∠MBC.∵DE、BF分别平分∠ADC、∠MBC,∴∠EDC=![]() ∠ADC,∠EBG=
∠ADC,∠EBG=![]() ∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
(2)DE∥BF.证明如下:
连接BD.∵DE、BF分别平分∠NDC、∠MBC,∴∠EDC=![]() ∠NDC,∠FBC=
∠NDC,∠FBC=![]() ∠MBC.
∠MBC.
∵∠ADC+∠NDC=180°,∠ADC=∠MBC,∴∠MBC+∠NDC=180°,∴∠EDC+∠FBC=90°.
∵∠C=90°,∴∠CDB+∠CBD=90°,∴∠EDC+∠CDB+∠FBC+∠CBD=180°,即∠EDB+∠FBD=180°,∴DE∥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可以坐6人,如果把多张桌子摆在一起,可以有以下两种摆放方式.
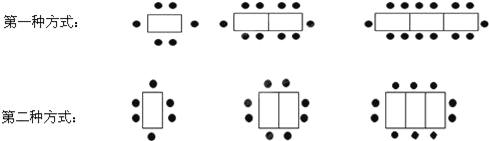
(1)当有5张桌子时,第一种摆放方式能坐 人,第二种摆放方式能坐 人,
(2)当有n张桌子时,第一种摆放方式能坐 人,第二种摆放方式能坐 人,
(3)一天中午餐厅要接待98位顾客共同就餐(即桌子要摆在一起),但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
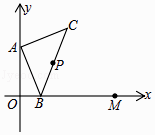
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点
 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米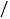 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米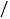 秒,则当△BPD与△CQP全等时,v的值为( )
秒,则当△BPD与△CQP全等时,v的值为( )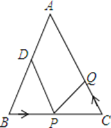
A. 2.5 B. 3 C. 2.25或3 D. 1或5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
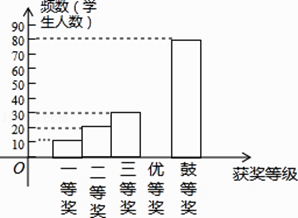
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
相关试题

