【题目】等腰三角形一腰上的高与底边的夹角为20°,则此三角形的顶角度数为_____.
参考答案:
【答案】40°.
【解析】
此题要分两种情况讨论:
(1)当等腰三角形的顶角是钝角时,腰上的高在三角形的外部,求出底角,再计算出顶角不是钝角,推出矛盾可知此情况不存在;
(2)当等腰三角形的顶角是锐角时,根据直角三角形的两个锐角互余,求得底角,再根据三角形的内角和是180°,可得顶角的度数.
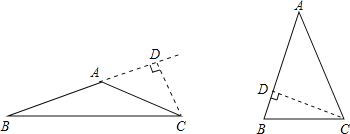
解:如图,分两种情况讨论:
(1)顶角是钝角时,由题意得:∠B=90°﹣20°=70°,
∴顶角=180°﹣2×70°=40°,不是钝角,故此情况不存在;
(2)顶角是锐角时,∠B=90°﹣20°=70°,
∠A=180°﹣2×70°=40°,是锐角,符合题意.
故答案为:40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且
 .
.(1)求证
 ;
;(2)当AB=12,AC=9,AE=8时,求BD的长与
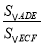 的值.
的值.
-
科目: 来源: 题型:
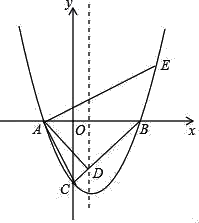
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(﹣2,0)、B(4,0),与y轴交于点C(0,﹣4),BC与抛物线的对称轴相交于点D.
(1)求该抛物线的表达式,并直接写出点D的坐标;
(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=5,AD=4,AD∥BM,
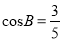 (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,
(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,  .
.(1)如图1,当x=4时,求AF的长;
(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
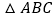 中,
中,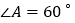 ,
,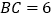 ,它的周长为
,它的周长为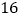 .若
.若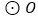 与
与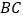 ,
,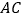 ,
,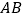 三边分别切于
三边分别切于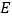 ,
, ,
, 点,则
点,则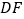 的长为( )
的长为( )
A.
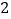 B.
B. 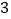 C.
C. 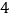 D.
D. 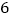
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等边三角形,将直角三角板DEF如图放置,其中∠F=30°,让△ABC在直角三角板的边EF上向右平移(点C与点F重合时停止).

(1)如图1,当点B与点E重合时,点A恰好落在直角三角板的斜边DF上,证明:EF=2BC.
(2)在△ABC平移过程中,AB,AC分别与三角板斜边的交点为G、H,如图2,线段EB=AH是否始终成立?如果成立,请证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①长度相等的弧是等弧;②平分弦的直径垂直于弦;③直径是弦;④同弧或等弧所对的圆心角相等;⑤在同圆或等圆中,相等的弦所对弧相等;错误的个数为( )
A.
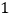 B.
B. 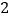 C.
C.  D.
D. 
相关试题

