【题目】已知,△ABC是等边三角形,将直角三角板DEF如图放置,其中∠F=30°,让△ABC在直角三角板的边EF上向右平移(点C与点F重合时停止).

(1)如图1,当点B与点E重合时,点A恰好落在直角三角板的斜边DF上,证明:EF=2BC.
(2)在△ABC平移过程中,AB,AC分别与三角板斜边的交点为G、H,如图2,线段EB=AH是否始终成立?如果成立,请证明;如果不成立,请说明理由.
参考答案:
【答案】(1)见解析;(2)成立.理由见解析.
【解析】
(1)根据等边三角形的性质,得∠ACB=60°,AC=BC.结合三角形外角的性质,得∠CAF=60°30°=30°,则CF=AC,从而证明结论;
(2)根据(1)中的证明方法,得到CH=CF.根据(1)中的结论,知EB+CF=AC,从而证明结论.
(1)∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵∠F=30°,
∴∠CAF=60°﹣30°=30°,
∴∠CAF=∠F,
∴CF=AC,
∴CF=AC=EC,
∴EF=2BC;
(2)线段EB=AH始终成立,
理由如下:
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵∠F=30°,
∴∠CHF=60°﹣30°=30°,
∴∠CHF=∠F,
∴CH=CF,
∵EF=2BC,
∴EB+CF=BC,
又∵AH+CH=AC,AC=BC,
∴EB=AH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=5,AD=4,AD∥BM,
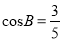 (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,
(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,  .
.(1)如图1,当x=4时,求AF的长;
(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与底边的夹角为20°,则此三角形的顶角度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
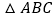 中,
中,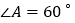 ,
,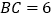 ,它的周长为
,它的周长为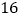 .若
.若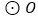 与
与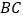 ,
,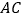 ,
,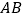 三边分别切于
三边分别切于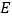 ,
, ,
, 点,则
点,则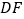 的长为( )
的长为( )
A.
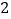 B.
B. 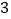 C.
C. 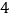 D.
D. 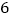
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①长度相等的弧是等弧;②平分弦的直径垂直于弦;③直径是弦;④同弧或等弧所对的圆心角相等;⑤在同圆或等圆中,相等的弦所对弧相等;错误的个数为( )
A.
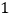 B.
B. 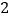 C.
C. 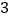 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
A.21B.42C.56D.84
-
科目: 来源: 题型:
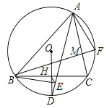
查看答案和解析>>【题目】如图,
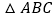 内接于
内接于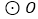 ,
, 是弧
是弧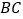 的中点,
的中点, 交
交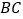 于点
于点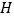 ,且
,且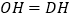 ,连接
,连接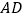 ,过点
,过点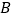 作
作 于点
于点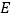 ,连接
,连接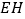 ,
, 于
于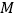 ,若
,若 ,
,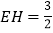 ,则
,则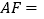 ________.
________.
相关试题

