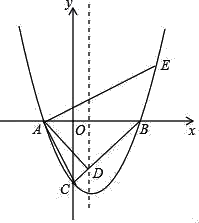
【题目】如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(﹣2,0)、B(4,0),与y轴交于点C(0,﹣4),BC与抛物线的对称轴相交于点D.
(1)求该抛物线的表达式,并直接写出点D的坐标;
(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标.
参考答案:
【答案】(1)y=![]() x2﹣x﹣4,D(1,﹣3);(2)E(5,
x2﹣x﹣4,D(1,﹣3);(2)E(5,![]() )
)
【解析】
(1)设抛物线的解析式为y=a(x+2)(x4), 将C(0,4)代入求解即可;记抛物线的对称轴与x轴交点坐标为F.先求得抛物线的对称轴,则可得到FB的长,然后再证明△BFD为等腰直角三角形,从而可得到FD=FB=3,故此可得到点D的坐标;
(2)过点E作EH⊥AB,垂足为H.先证∠EAH=∠ACO,则tan∠EAH=tan∠ACO=![]() .设EH=t,则AH=2t,从而可得到E(-2+2t,t),最后,将点E的坐标代入抛物线的解析式求解即可;
.设EH=t,则AH=2t,从而可得到E(-2+2t,t),最后,将点E的坐标代入抛物线的解析式求解即可;
(1)设抛物线的解析式为y=a(x+2)(x4),将C(0,4)代入得:8a=4,解得:![]()
∴抛物线的解析式为![]()
如下图所示:记抛物线的对称轴与x轴交点坐标为F.
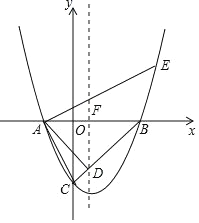
∵抛物线的对称轴为![]()
∴BF=OBOF=3.
∵BO=OC=4,![]()
∴![]()
∴△BFD为等腰直角三角形,
∴FD=FB=3.
∴D(1,3).
(2)如下图,过点E作EH⊥AB,垂足为H.
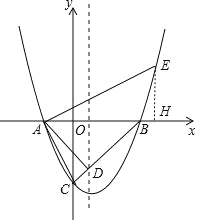
∵![]()
∴∠EAH=∠ACO.
∴tan∠EAH=tan∠ACO=![]() .
.
设EH=t,则AH=2t,
∴点E的坐标为(2+2t,t).
将(2+2t,t)代入抛物线的解析式得:![]()
解得:![]() 或t=0(舍去)
或t=0(舍去)
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且
 .
.(1)求证
 ;
;(2)当AB=12,AC=9,AE=8时,求BD的长与
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=5,AD=4,AD∥BM,
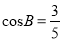 (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,
(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,  .
.(1)如图1,当x=4时,求AF的长;
(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与底边的夹角为20°,则此三角形的顶角度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
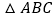 中,
中,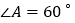 ,
,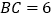 ,它的周长为
,它的周长为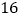 .若
.若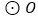 与
与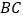 ,
,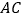 ,
,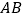 三边分别切于
三边分别切于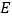 ,
, ,
, 点,则
点,则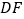 的长为( )
的长为( )
A.
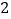 B.
B. 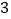 C.
C. 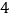 D.
D. 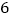
相关试题

