【题目】如图,直线l:y=x﹣![]() 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=![]() x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.
(1)填空:直接写出抛物线的解析式:_____;
(2)已知点Q是抛物线y=![]() x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.
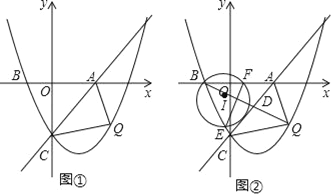
①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
参考答案:
【答案】(1)![]() (2)①
(2)①![]() ,
, ![]()
![]() ,②
,②![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
【解析】试题分析:(1)令![]() ,求出直线
,求出直线![]() 与y轴的交点即C点坐标,再用待定系数法求二次函数解析式即可;(2)①在直线
与y轴的交点即C点坐标,再用待定系数法求二次函数解析式即可;(2)①在直线![]() 中,令
中,令![]() ,得到点A的坐标,连接
,得到点A的坐标,连接![]() ,由
,由![]() 即可得到
即可得到![]() 与
与![]() 的函数关系;②由点
的函数关系;②由点![]() 得
得![]() . 作直径
. 作直径![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 时,此时直径
时,此时直径![]() 最小,即直径
最小,即直径![]() 最小,
最小, ![]() 的值最小.
的值最小. ![]() ,
, ![]() =
= ![]() =
=![]() ,
,
求出点![]() 的坐标.
的坐标.
试题解析:(1)在直线![]() 中,令
中,令![]() ,则
,则![]() ,∴点
,∴点![]()
把点![]() 与点
与点![]() 代入
代入![]() ,得:
,得:  ,解得:
,解得: 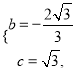 ,
,
∴抛物线的解析式为: ![]() .
.
(2) ①连接![]() ,在直线
,在直线![]() 中,令
中,令![]() ,则
,则![]() ,
,

∴点![]() .
.
∵![]() ,
,
∴ ,
,
∴![]() ,
,
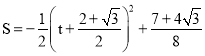 ,
, ![]() .
.
∴当![]() 时,
时, ![]() .
.
②∵![]() ∴
∴![]() ,
, ![]() .
.
在![]() 中,
中, ![]()
∴![]() .
.
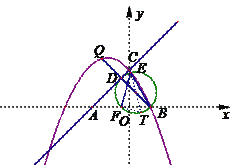
作直径![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,
,
又![]() ,
, ![]() ,
,
![]() ,
,
当![]() 时,此时直径
时,此时直径![]() 最小,即直径
最小,即直径![]() 最小,
最小, ![]() 的值最小.
的值最小.
![]() ,
,
∴![]() ,
,
![]()
∴![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x
1
2
5
10
20
舒适度指数y
100
50
20
10
5
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球上的海洋面积约为36105.9万平方千米,用科学记数法(保留三个有效数字)表示为平方千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列三角形中:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中是等边三角形的有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
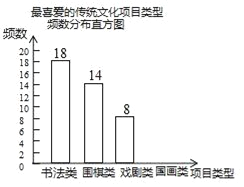
查看答案和解析>>【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
项目类型
频数
频率
书法类
18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
根据以上信息完成下列问题:
(1)频数分布表中a=_____,b=_____;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若点(﹣
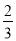 ,y1)和(
,y1)和(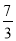 ,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)
,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)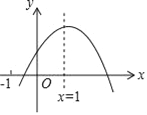
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD=BD=BC,则∠A的度数是( )
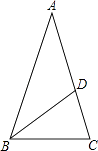
A.30°
B.36°
C.45°
D.20°
相关试题

