【题目】如图,∠ABC=∠ADC=90°,∠BAD=45°,E、F分别是AC、BD的中点.若AC=2,求EF的长.

参考答案:
【答案】![]() .
.
【解析】
连接BE、DE,利用直角三角形斜边的中线等于斜边的一半证明BED为等腰三角形,再根据外角定理证明∠BED为90°,则△BED为等腰直角三角形,再根据勾股定理即可求出.
连接BE、DE,
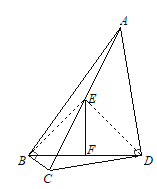
∵∠ABC=∠ADC=90°,E为AC中点,
∴BE=![]() ,DE=
,DE=![]() ,△AEB和△AED是全等三角形.
,△AEB和△AED是全等三角形.
∴∠BEC=2∠BAE,∠DEC=2∠DAE;
∴∠BED=∠BEC+∠DEC=2∠BAE+2∠DAE=2(∠BAE+∠BAE)=2∠BAD=90°;
又∵BE=DE
∴△BED是等腰直角三角形.
∵AC=2,
∴BE=ED=1,
又∵F是BD的中点,
∴EF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在等边三角形
 中,
中, 是
是 边上的动点,以
边上的动点,以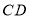 为一边,向上作等边三角形
为一边,向上作等边三角形 ,连接
,连接 .
.(1)
 和
和 全等吗?请说明理由;
全等吗?请说明理由;(2)试说明:
 ;
;(3)如图(2),将动点
 运动到边
运动到边 的延长线上,所作三角形
的延长线上,所作三角形 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有 ?请说明理由.
?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 轴上,
轴上, ,
, ,
, ,将
,将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到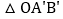 ,则点
,则点 的坐标是( )
的坐标是( )
A. (2,-2
 ) B. (2,-2
) B. (2,-2 ) C. (2
) C. (2 ,2) D. (2
,2) D. (2 ,2)
,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为3和7,则△CDE的面积为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(10,0),B(10,6),BC⊥y轴,垂足为C,点D在线段BC上,且AD=AO.
(1)试说明:DO平分∠CDA;
(2)求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )

A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在四边形ABCD中,AB=BC=CD=DA=5 cm,BD=8 cm.则AC= cm;
(2)在宽为8 cm 的长方形纸带上,用图1中的四边形设计如图2所示的图案.
①如果用7个图1中的四边形设计图案,那么至少需要 cm长的纸带;
②设图1中的四边形有x个,所需的纸带长为y cm,求y与x之间的函数表达式;
③在长为40 cm的纸带上,按照这种方法,最多能设计多少个图1中的四边形?

相关试题

