【题目】（1）如图1，在四边形ABCD中，AB=BC=CD=DA=5 cm，BD=8 cm．则AC= cm；

（2）在宽为8 cm 的长方形纸带上，用图1中的四边形设计如图2所示的图案．

①如果用7个图1中的四边形设计图案，那么至少需要 cm长的纸带；

②设图1中的四边形有x个，所需的纸带长为y cm，求y与x之间的函数表达式；

③在长为40 cm的纸带上，按照这种方法，最多能设计多少个图1中的四边形？

参考答案：

【答案】(1)6;(2)①20,②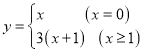,③12.

【解析】

(1)由题意得,四边形为菱形,根据菱形的性质利用勾股定理解出即可.

(2)①通过前三个四边形寻找规律即可解出.②利用①中的规律表示出来即可.③令y≤40解出x的范围,即可找到最大的值.

(1)设AC与BD的交点为O,

∵AB=BC=CD=DA=5 cm,

∴四边形ABCD为菱形,

∴OD=,AB⊥AC,

∴OC=.

∴AC=6.

(2)①由图可知:1个四边形需要2×3=6cm,2个四边形需要3×3=9cm,3个四边形需要4×3=20cm……,

所以7个四边形需要8×3=24cm长的纸带.

②由①中规律可得:.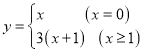

③将y≤40代入②的表达式中,可得x≤.

所以最多能设计12个四边形.

关闭