【题目】如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为3和7,则△CDE的面积为_________.

参考答案:
【答案】![]() .
.
【解析】
过E作EH⊥CD于H,根据角之间的等量关系可得到∠1=∠3,从而可利用AAS判定△EDH≌△DGA,由全等三角形的性质可得EH=AG,根据正方形的面积求角其边长,从而利用勾股定理求得AG的长,再根据三角形的面积公式求解即可.
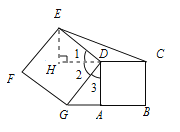
过E作EH⊥CD于H,如图,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
又∵∠EHD=∠DAG=90°,ED=DG,
∴△EDH≌△DGA,
∴EH=AG,
∵SABCD=7cm2,SDGFE=11cm2,
∴CD=AD=![]() cm,DG=
cm,DG=![]() cm,
cm,
∴在Rt△ADG中,AG=![]() =
=![]() =2(cm),
=2(cm),
∴S△CDE=![]() CD×EH=
CD×EH=![]() CD×AG=
CD×AG=![]() ×
×![]() ×2=
×2=![]() cm2,
cm2,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是锐角三角形
是锐角三角形 内一点,
内一点, ,
,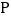 是
是 内不同于
内不同于 的另一点;
的另一点; 、
、 分别由
分别由 、
、 逆时针旋转而得,旋转角都为
逆时针旋转而得,旋转角都为 ,则下列结论:
,则下列结论:①
 .
.②
 、
、 、
、 、
、 在一条直线上.
在一条直线上.③
 .
.④
 .
.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在等边三角形
 中,
中, 是
是 边上的动点,以
边上的动点,以 为一边,向上作等边三角形
为一边,向上作等边三角形 ,连接
,连接 .
.(1)
 和
和 全等吗?请说明理由;
全等吗?请说明理由;(2)试说明:
 ;
;(3)如图(2),将动点
 运动到边
运动到边 的延长线上,所作三角形
的延长线上,所作三角形 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有 ?请说明理由.
?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 轴上,
轴上, ,
, ,
, ,将
,将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到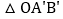 ,则点
,则点 的坐标是( )
的坐标是( )
A. (2,-2
 ) B. (2,-2
) B. (2,-2 ) C. (2
) C. (2 ,2) D. (2
,2) D. (2 ,2)
,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ADC=90°,∠BAD=45°,E、F分别是AC、BD的中点.若AC=2,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(10,0),B(10,6),BC⊥y轴,垂足为C,点D在线段BC上,且AD=AO.
(1)试说明:DO平分∠CDA;
(2)求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )

A.4个 B.3个 C.2个 D.1个
相关试题

